
Question Number 182694 by cherokeesay last updated on 13/Dec/22

Answered by HeferH last updated on 13/Dec/22
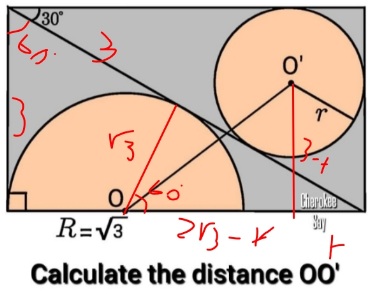
Commented by HeferH last updated on 13/Dec/22
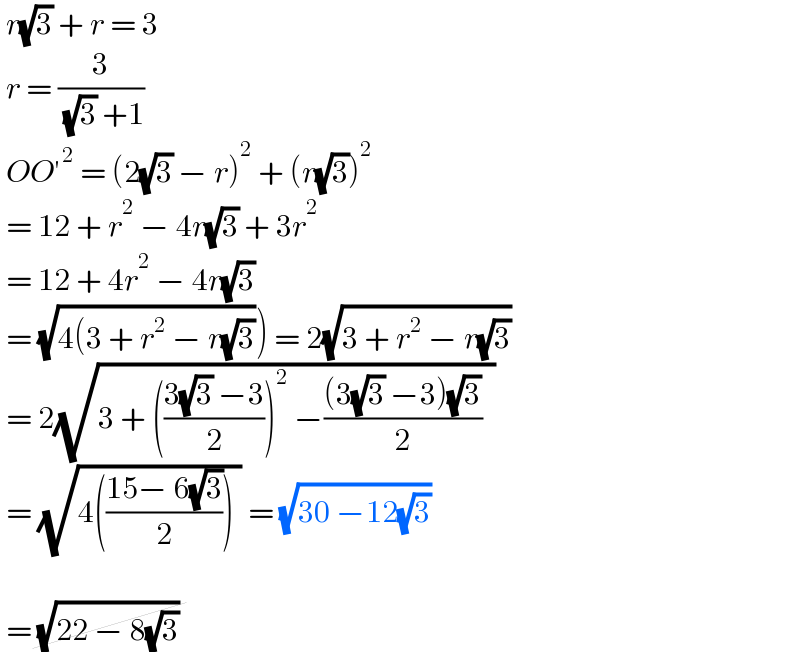
$$\:{r}\sqrt{\mathrm{3}}\:+\:{r}\:=\:\mathrm{3} \\ $$$$\:{r}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{3}}\:+\mathrm{1}} \\ $$$$\:{OO}'^{\mathrm{2}} \:=\:\left(\mathrm{2}\sqrt{\mathrm{3}}\:−\:{r}\right)^{\mathrm{2}} \:+\:\left({r}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:=\:\mathrm{12}\:+\:{r}^{\mathrm{2}} \:−\:\mathrm{4}{r}\sqrt{\mathrm{3}}\:+\:\mathrm{3}{r}^{\mathrm{2}} \\ $$$$\:=\:\mathrm{12}\:+\:\mathrm{4}{r}^{\mathrm{2}} \:−\:\mathrm{4}{r}\sqrt{\mathrm{3}} \\ $$$$\left.\:=\:\sqrt{\mathrm{4}\left(\mathrm{3}\:+\:{r}^{\mathrm{2}} \:−\:{r}\sqrt{\mathrm{3}}\right.}\right)\:=\:\mathrm{2}\sqrt{\mathrm{3}\:+\:{r}^{\mathrm{2}} \:−\:{r}\sqrt{\mathrm{3}}}\: \\ $$$$\:=\:\mathrm{2}\sqrt{\mathrm{3}\:+\:\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}\:−\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \:−\frac{\left(\mathrm{3}\sqrt{\mathrm{3}}\:−\mathrm{3}\right)\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:} \\ $$$$\:=\:\sqrt{\mathrm{4}\left(\frac{\mathrm{15}−\:\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:}\:=\:\sqrt{\mathrm{30}\:−\mathrm{12}\sqrt{\mathrm{3}}}\: \\ $$$$\: \\ $$$$\:=\cancel{\:\sqrt{\mathrm{22}\:−\:\mathrm{8}\sqrt{\mathrm{3}}}\:} \\ $$
Commented by cherokeesay last updated on 13/Dec/22
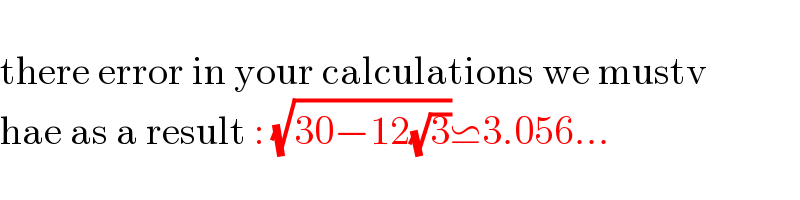
$$ \\ $$$$\mathrm{there}\:\mathrm{error}\:\mathrm{in}\:\mathrm{your}\:\mathrm{calculations}\:\mathrm{we}\:\mathrm{mustv} \\ $$$$\mathrm{hae}\:\mathrm{as}\:\mathrm{a}\:\mathrm{result}\::\:\sqrt{\mathrm{30}−\mathrm{12}\sqrt{\mathrm{3}}}\backsimeq\mathrm{3}.\mathrm{056}... \\ $$
Commented by HeferH last updated on 13/Dec/22
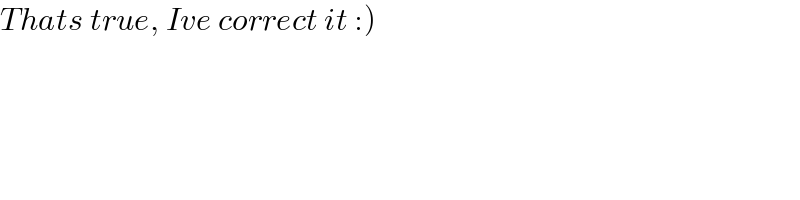
$$\left.{Thats}\:{true},\:{Ive}\:{correct}\:{it}\::\right) \\ $$
