
Question Number 18268 by Tinkutara last updated on 17/Jul/17

$$\mathrm{A}\:\mathrm{balloon}\:\mathrm{starts}\:\mathrm{rising}\:\mathrm{from}\:\mathrm{the}\:\mathrm{surface} \\ $$$$\mathrm{of}\:\mathrm{earth}.\:\mathrm{The}\:\mathrm{ascension}\:\mathrm{rate}\:\mathrm{is}\:\mathrm{constant} \\ $$$$\mathrm{and}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:{v}_{\mathrm{0}} .\:\mathrm{Due}\:\mathrm{to}\:\mathrm{wind}\:\mathrm{the} \\ $$$$\mathrm{balloon}\:\mathrm{gathers}\:\mathrm{horizontal}\:\mathrm{velocity} \\ $$$$\mathrm{component}\:{v}_{{x}} \:=\:{ay},\:\mathrm{where}\:{a}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positive} \\ $$$$\mathrm{constant}\:\mathrm{and}\:{y}\:\mathrm{is}\:\mathrm{the}\:\mathrm{height}\:\mathrm{of}\:\mathrm{ascent}. \\ $$$$\mathrm{Find} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{The}\:\mathrm{horizontal}\:\mathrm{drift}\:\mathrm{of}\:\mathrm{the}\:\mathrm{balloon} \\ $$$${x}\left({y}\right), \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{The}\:\mathrm{total},\:\mathrm{tangential}\:\mathrm{and}\:\mathrm{normal} \\ $$$$\mathrm{accelerations}\:\mathrm{of}\:\mathrm{the}\:\mathrm{balloon}. \\ $$
Answered by ajfour last updated on 16/Aug/17
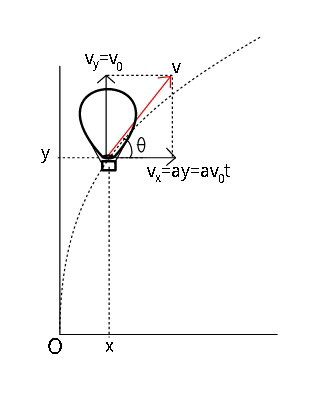
Commented by Tinkutara last updated on 17/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 16/Aug/17
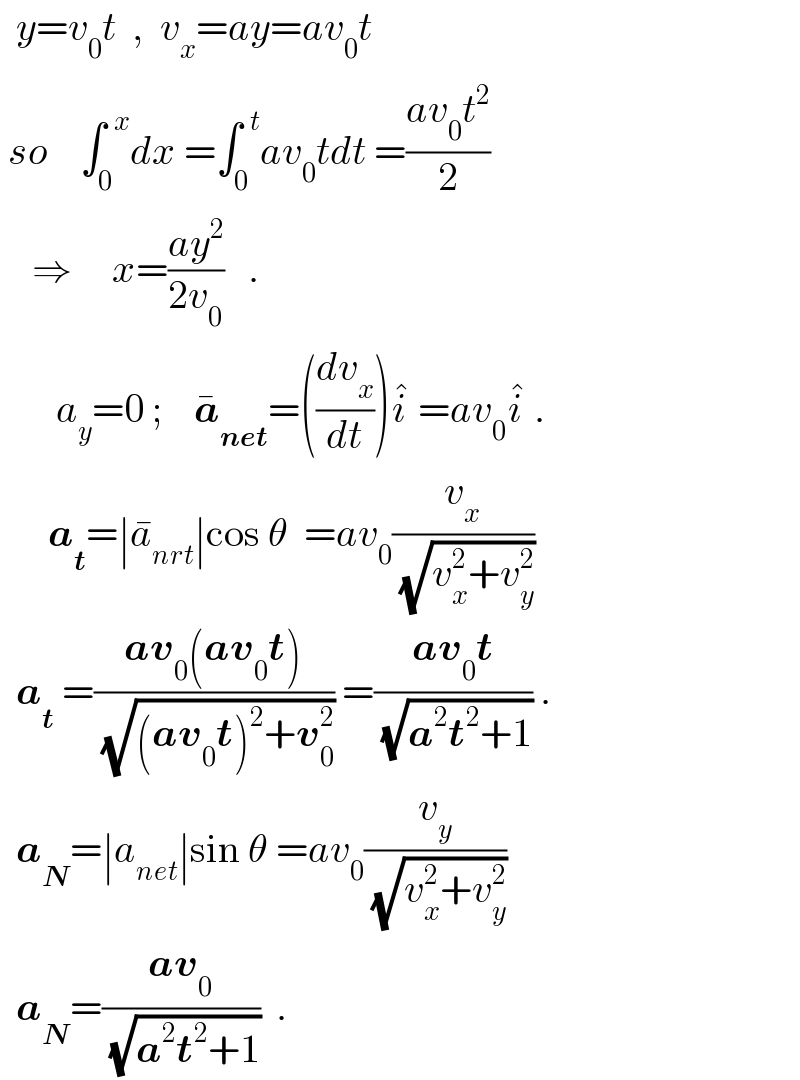
$$\:\:{y}={v}_{\mathrm{0}} {t}\:\:,\:\:{v}_{{x}} ={ay}={av}_{\mathrm{0}} {t} \\ $$$$\:{so}\:\:\:\:\int_{\mathrm{0}} ^{\:\:{x}} {dx}\:=\int_{\mathrm{0}} ^{\:\:{t}} {av}_{\mathrm{0}} {tdt}\:=\frac{{av}_{\mathrm{0}} {t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:\Rightarrow\:\:\:\:\:{x}=\frac{{ay}^{\mathrm{2}} }{\mathrm{2}{v}_{\mathrm{0}} }\:\:\:. \\ $$$$\:\:\:\:\:\:\:{a}_{{y}} =\mathrm{0}\:;\:\:\:\:\bar {\boldsymbol{{a}}}_{\boldsymbol{{net}}} =\left(\frac{{dv}_{{x}} }{{dt}}\right)\hat {{i}}\:={av}_{\mathrm{0}} \hat {{i}}\:. \\ $$$$\:\:\:\:\:\:\boldsymbol{{a}}_{\boldsymbol{{t}}} =\mid\bar {{a}}_{{nrt}} \mid\mathrm{cos}\:\theta\:\:={av}_{\mathrm{0}} \frac{{v}_{{x}} }{\sqrt{{v}_{{x}} ^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} }}\: \\ $$$$\:\:\boldsymbol{{a}}_{\boldsymbol{{t}}} \:=\frac{\boldsymbol{{av}}_{\mathrm{0}} \left(\boldsymbol{{av}}_{\mathrm{0}} \boldsymbol{{t}}\right)}{\sqrt{\left(\boldsymbol{{av}}_{\mathrm{0}} \boldsymbol{{t}}\right)^{\mathrm{2}} +\boldsymbol{{v}}_{\mathrm{0}} ^{\mathrm{2}} }}\:=\frac{\boldsymbol{{av}}_{\mathrm{0}} \boldsymbol{{t}}}{\sqrt{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{t}}^{\mathrm{2}} +\mathrm{1}}}\:. \\ $$$$\:\:\boldsymbol{{a}}_{\boldsymbol{{N}}} =\mid{a}_{{net}} \mid\mathrm{sin}\:\theta\:={av}_{\mathrm{0}} \frac{{v}_{{y}} }{\sqrt{{v}_{{x}} ^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} }}\: \\ $$$$\:\:\boldsymbol{{a}}_{\boldsymbol{{N}}} =\frac{\boldsymbol{{av}}_{\mathrm{0}} }{\sqrt{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{t}}^{\mathrm{2}} +\mathrm{1}}}\:\:. \\ $$
