
Question Number 182593 by srikanth2684 last updated on 11/Dec/22

Commented by srikanth2684 last updated on 14/Dec/22

$${sol}\:{pls} \\ $$
Answered by TheSupreme last updated on 15/Dec/22
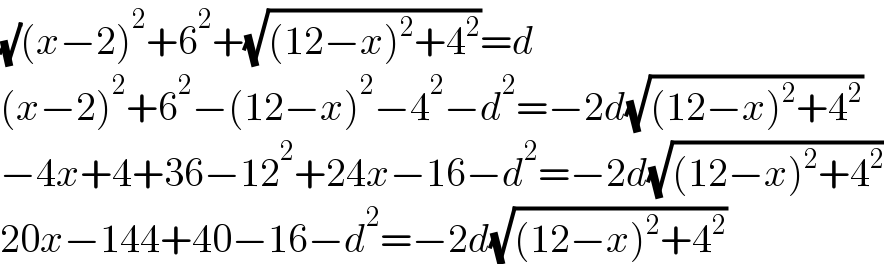
$$\sqrt{}\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} +\sqrt{\left(\mathrm{12}−{x}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }={d} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\left(\mathrm{12}−{x}\right)^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} −{d}^{\mathrm{2}} =−\mathrm{2}{d}\sqrt{\left(\mathrm{12}−{x}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} } \\ $$$$−\mathrm{4}{x}+\mathrm{4}+\mathrm{36}−\mathrm{12}^{\mathrm{2}} +\mathrm{24}{x}−\mathrm{16}−{d}^{\mathrm{2}} =−\mathrm{2}{d}\sqrt{\left(\mathrm{12}−{x}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} } \\ $$$$\mathrm{20}{x}−\mathrm{144}+\mathrm{40}−\mathrm{16}−{d}^{\mathrm{2}} =−\mathrm{2}{d}\sqrt{\left(\mathrm{12}−{x}\right)^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} } \\ $$
