
Question Number 182546 by Acem last updated on 11/Dec/22

Commented by Acem last updated on 11/Dec/22
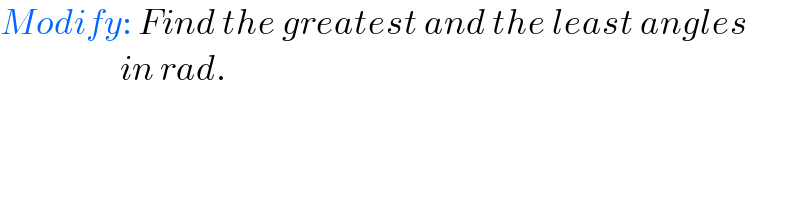
$${Modify}:\:{Find}\:{the}\:{greatest}\:{and}\:{the}\:{least}\:{angles} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{in}\:{rad}. \\ $$
Answered by Rasheed.Sindhi last updated on 11/Dec/22
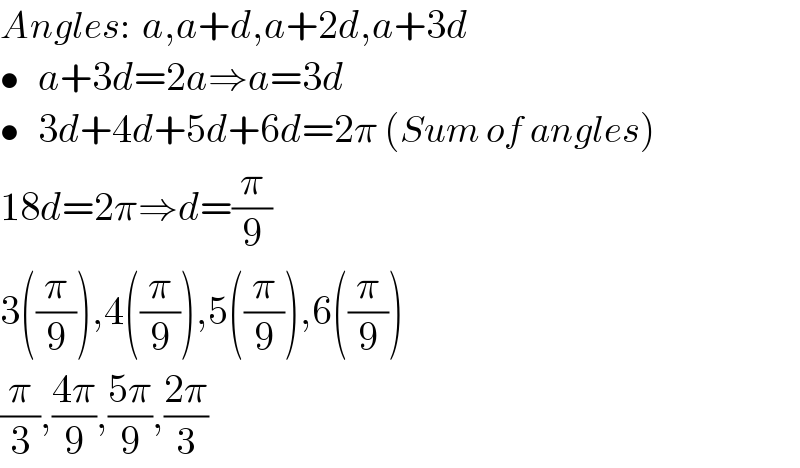
$${Angles}:\:\:{a},{a}+{d},{a}+\mathrm{2}{d},{a}+\mathrm{3}{d} \\ $$$$\bullet\:\:\:{a}+\mathrm{3}{d}=\mathrm{2}{a}\Rightarrow{a}=\mathrm{3}{d} \\ $$$$\bullet\:\:\:\mathrm{3}{d}+\mathrm{4}{d}+\mathrm{5}{d}+\mathrm{6}{d}=\mathrm{2}\pi\:\left({Sum}\:{of}\:{angles}\right) \\ $$$$\mathrm{18}{d}=\mathrm{2}\pi\Rightarrow{d}=\frac{\pi}{\mathrm{9}} \\ $$$$\mathrm{3}\left(\frac{\pi}{\mathrm{9}}\right),\mathrm{4}\left(\frac{\pi}{\mathrm{9}}\right),\mathrm{5}\left(\frac{\pi}{\mathrm{9}}\right),\mathrm{6}\left(\frac{\pi}{\mathrm{9}}\right) \\ $$$$\frac{\pi}{\mathrm{3}},\frac{\mathrm{4}\pi}{\mathrm{9}},\frac{\mathrm{5}\pi}{\mathrm{9}},\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$
Commented by Acem last updated on 11/Dec/22
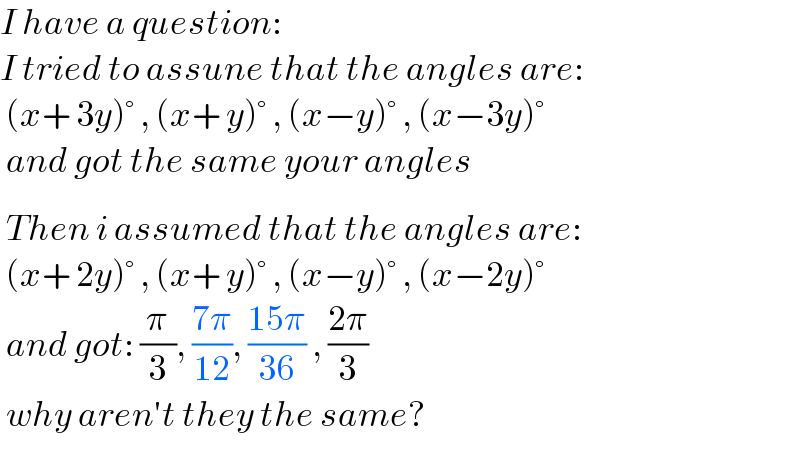
$${I}\:{have}\:{a}\:{question}: \\ $$$${I}\:{tried}\:{to}\:{assune}\:{that}\:{the}\:{angles}\:{are}: \\ $$$$\:\left({x}+\:\mathrm{3}{y}\right)°\:,\:\left({x}+\:{y}\right)°\:,\:\left({x}−{y}\right)°\:,\:\left({x}−\mathrm{3}{y}\right)° \\ $$$$\:{and}\:{got}\:{the}\:{same}\:{your}\:{angles} \\ $$$$ \\ $$$$\:{Then}\:{i}\:{assumed}\:{that}\:{the}\:{angles}\:{are}: \\ $$$$\:\left({x}+\:\mathrm{2}{y}\right)°\:,\:\left({x}+\:{y}\right)°\:,\:\left({x}−{y}\right)°\:,\:\left({x}−\mathrm{2}{y}\right)° \\ $$$$\:{and}\:{got}:\:\frac{\pi}{\mathrm{3}},\:\frac{\mathrm{7}\pi}{\mathrm{12}},\:\frac{\mathrm{15}\pi}{\mathrm{36}}\:,\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\:{why}\:{aren}'{t}\:{they}\:{the}\:{same}? \\ $$$$\: \\ $$
Commented by mr W last updated on 11/Dec/22

$${in}\:{way}\:\mathrm{1}\:{the}\:{difference}\:{between}\:{any}\: \\ $$$${two}\:{consecutive}\:{terms}\:{is}\:−\mathrm{2}{y}.\:{that}'{s} \\ $$$${correct}. \\ $$$${in}\:{way}\:\mathrm{2}\:{the}\:{difference}\:{between}\:{the} \\ $$$${first}\:{and}\:{the}\:{second}\:{term}\:{as}\:{well}\:{as}\: \\ $$$${between}\:{the}\:{third}\:{and}\:{fourth}\:{term} \\ $$$${is}\:−{y},\:{but}\:{it}'{s}\:−\mathrm{2}{y}\:{between}\:{the}\:{second}\:{and} \\ $$$${the}\:{third}\:{term}.\:{this}\:{is}\:{not}\:{a}\:{A}.{P}.\:! \\ $$
Commented by Rasheed.Sindhi last updated on 11/Dec/22
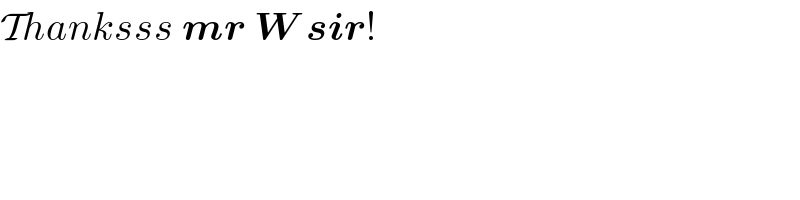
$$\mathcal{T}{hanksss}\:\boldsymbol{{mr}}\:\boldsymbol{{W}}\:\boldsymbol{{sir}}! \\ $$
Answered by manxsol last updated on 11/Dec/22
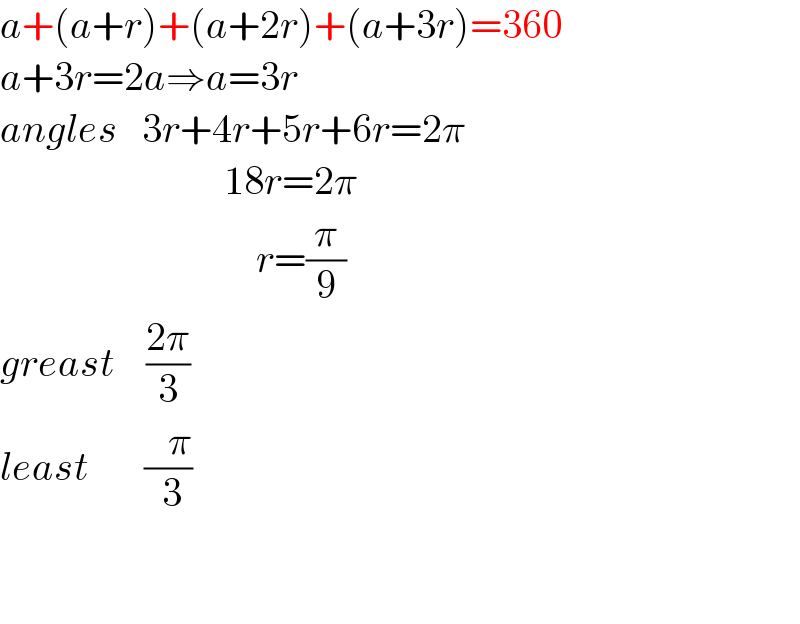
$${a}+\left({a}+{r}\right)+\left({a}+\mathrm{2}{r}\right)+\left({a}+\mathrm{3}{r}\right)=\mathrm{360} \\ $$$${a}+\mathrm{3}{r}=\mathrm{2}{a}\Rightarrow{a}=\mathrm{3}{r} \\ $$$${angles}\:\:\:\mathrm{3}{r}+\mathrm{4}{r}+\mathrm{5}{r}+\mathrm{6}{r}=\mathrm{2}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{18}{r}=\mathrm{2}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}=\frac{\pi}{\mathrm{9}} \\ $$$${greast}\:\:\:\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${least}\:\:\:\:\:\:\:\frac{\:\:\:\pi}{\:\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
Commented by Acem last updated on 11/Dec/22

$${Thanksss}! \\ $$
