
Question Number 182500 by mr W last updated on 10/Dec/22
Commented by mr W last updated on 10/Dec/22

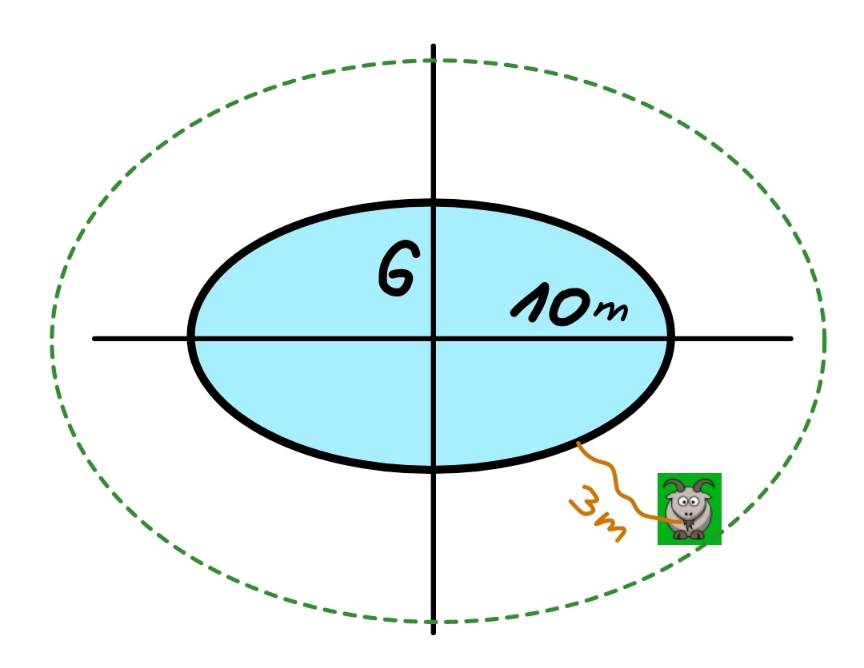
$${this}\:{time}\:{our}\:{goat}\:{is}\:{flexibly}\:{tied}\:{on} \\ $$$${a}\:{fence}\:{with}\:{a}\:{rope}\:{of}\:{length}\:\mathrm{3}{m}.\:{the} \\ $$$${fence}\:{has}\:{the}\:{shape}\:{of}\:{an}\:{ellipse}\:{with} \\ $$$${semi}−{axex}\:{of}\:\mathrm{10}\:{m}\:{and}\:\mathrm{6}\:{m}\:{respectively}. \\ $$$${find}\:{the}\:{maximum}\:{area}\:{where}\:{the} \\ $$$${goat}\:{can}\:{graze}. \\ $$
Answered by mr W last updated on 10/Dec/22
Commented by mr W last updated on 10/Dec/22
![a=10, b=6, c=3 let μ=(b/a), λ=(c/a) say P(a cos φ, b sin φ) −(1/(tan θ))=((b cos φ)/(−a sin θ)) ⇒tan θ=((tan φ)/μ) x_Q =a cos φ+c cos θ y_Q =b sin φ+c sin θ (x_Q /a)=ξ=cos φ+((λμ)/( (√(μ^2 +tan^2 φ)))) (y_Q /a)=η=μ sin φ+((λ tan φ)/( (√(μ^2 +tan^2 φ)))) A_I =∫y_Q dx_Q (A_I /a^2 )=∫ηdξ=∫_0 ^(π/2) (μ sin φ+((λ tan φ)/( (√(μ^2 +tan^2 φ)))))(sin φ+((λμ tan φ)/(cos^2 φ (μ^2 +tan^2 φ)^(3/2) )))dφ=δ δ=∫_0 ^(π/2) (μ sin φ+((λ tan φ)/( (√(μ^2 +tan^2 φ)))))(sin φ+((λμ tan φ)/(cos^2 φ (μ^2 +tan^2 φ)^(3/2) )))dφ A_(grazing) =4A_I −πab=4δa^2 −πab A_(grazing) =(((4δ)/μ)−π)ab example: μ=(6/(10))=0.6, λ=(3/(10))=0.3 δ≈0.924 829 716 A_(grazing) =(((4δ)/(0.6))−π)×60≈181.436 m^2 an approximation as ellipse is A_(grazing) ≈π[(a+c)(b+c)−ab]=π(a+b+c)c =(10+6+3)π=179.07 m^2](Q182515.png)
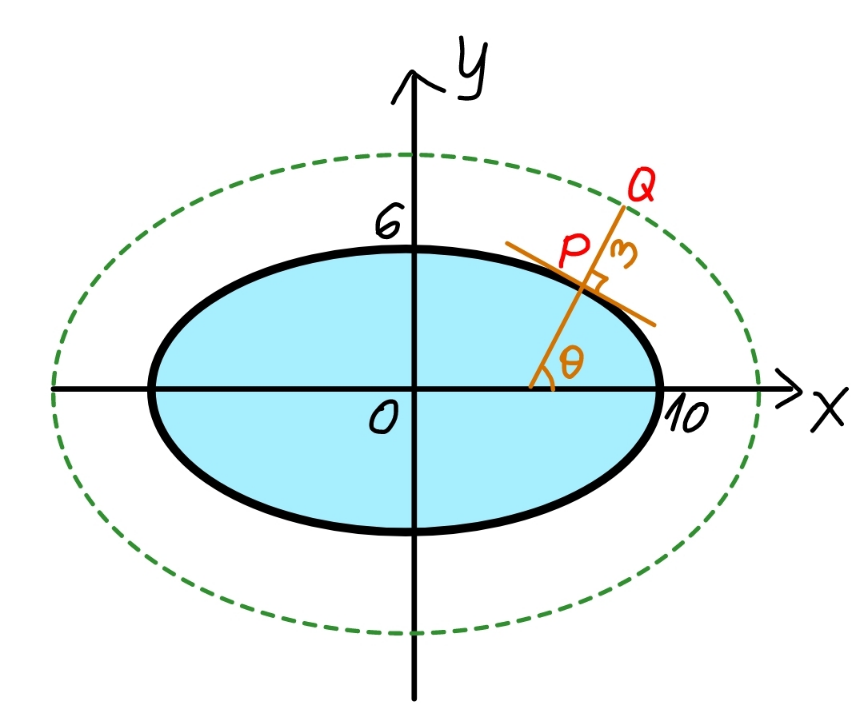
$${a}=\mathrm{10},\:{b}=\mathrm{6},\:{c}=\mathrm{3} \\ $$$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{c}}{{a}} \\ $$$${say}\:{P}\left({a}\:\mathrm{cos}\:\phi,\:{b}\:\mathrm{sin}\:\phi\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\frac{{b}\:\mathrm{cos}\:\phi}{−{a}\:\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{tan}\:\phi}{\mu} \\ $$$${x}_{{Q}} ={a}\:\mathrm{cos}\:\phi+{c}\:\mathrm{cos}\:\theta \\ $$$${y}_{{Q}} ={b}\:\mathrm{sin}\:\phi+{c}\:\mathrm{sin}\:\theta \\ $$$$\frac{{x}_{{Q}} }{{a}}=\xi=\mathrm{cos}\:\phi+\frac{\lambda\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi}} \\ $$$$\frac{{y}_{{Q}} }{{a}}=\eta=\mu\:\mathrm{sin}\:\phi+\frac{\lambda\:\mathrm{tan}\:\phi}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi}} \\ $$$${A}_{{I}} =\int{y}_{{Q}} {dx}_{{Q}} \\ $$$$\frac{{A}_{{I}} }{{a}^{\mathrm{2}} }=\int\eta{d}\xi=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mu\:\mathrm{sin}\:\phi+\frac{\lambda\:\mathrm{tan}\:\phi}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi}}\right)\left(\mathrm{sin}\:\phi+\frac{\lambda\mu\:\mathrm{tan}\:\phi}{\mathrm{cos}^{\mathrm{2}} \:\phi\:\left(\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi\right)^{\mathrm{3}/\mathrm{2}} }\right){d}\phi=\delta \\ $$$$\delta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mu\:\mathrm{sin}\:\phi+\frac{\lambda\:\mathrm{tan}\:\phi}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi}}\right)\left(\mathrm{sin}\:\phi+\frac{\lambda\mu\:\mathrm{tan}\:\phi}{\mathrm{cos}^{\mathrm{2}} \:\phi\:\left(\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi\right)^{\mathrm{3}/\mathrm{2}} }\right){d}\phi \\ $$$${A}_{{grazing}} =\mathrm{4}{A}_{{I}} −\pi{ab}=\mathrm{4}\delta{a}^{\mathrm{2}} −\pi{ab} \\ $$$${A}_{{grazing}} =\left(\frac{\mathrm{4}\delta}{\mu}−\pi\right){ab} \\ $$$${example}: \\ $$$$\mu=\frac{\mathrm{6}}{\mathrm{10}}=\mathrm{0}.\mathrm{6},\:\lambda=\frac{\mathrm{3}}{\mathrm{10}}=\mathrm{0}.\mathrm{3} \\ $$$$\delta\approx\mathrm{0}.\mathrm{924}\:\mathrm{829}\:\mathrm{716} \\ $$$${A}_{{grazing}} =\left(\frac{\mathrm{4}\delta}{\mathrm{0}.\mathrm{6}}−\pi\right)×\mathrm{60}\approx\mathrm{181}.\mathrm{436}\:{m}^{\mathrm{2}} \\ $$$$ \\ $$$${an}\:{approximation}\:{as}\:{ellipse}\:{is} \\ $$$${A}_{{grazing}} \approx\pi\left[\left({a}+{c}\right)\left({b}+{c}\right)−{ab}\right]=\pi\left({a}+{b}+{c}\right){c} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{10}+\mathrm{6}+\mathrm{3}\right)\pi=\mathrm{179}.\mathrm{07}\:{m}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 10/Dec/22
Commented by mr W last updated on 10/Dec/22
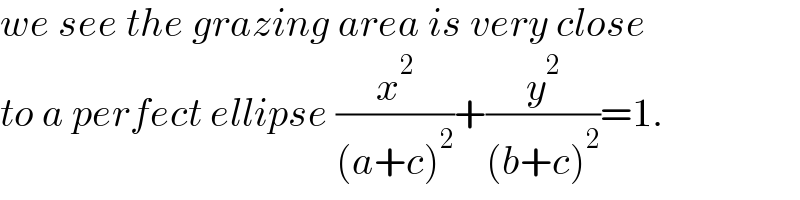
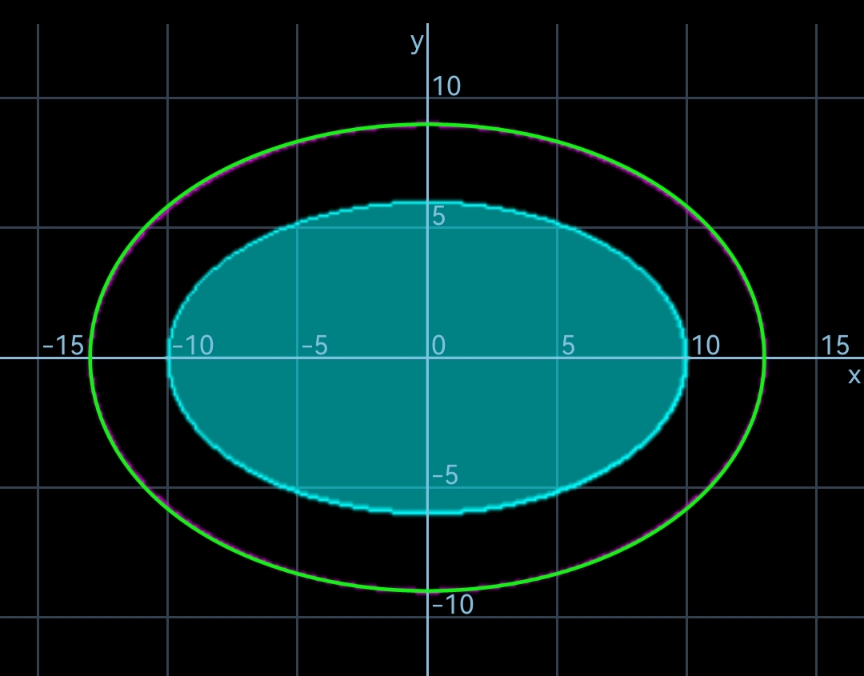
$${we}\:{see}\:{the}\:{grazing}\:{area}\:{is}\:{very}\:{close} \\ $$$${to}\:{a}\:{perfect}\:{ellipse}\:\frac{{x}^{\mathrm{2}} }{\left({a}+{c}\right)^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\left({b}+{c}\right)^{\mathrm{2}} }=\mathrm{1}. \\ $$
Commented by Acem last updated on 10/Dec/22

$${So}\:{nice} \\ $$
