
Question Number 182461 by HeferH last updated on 09/Dec/22
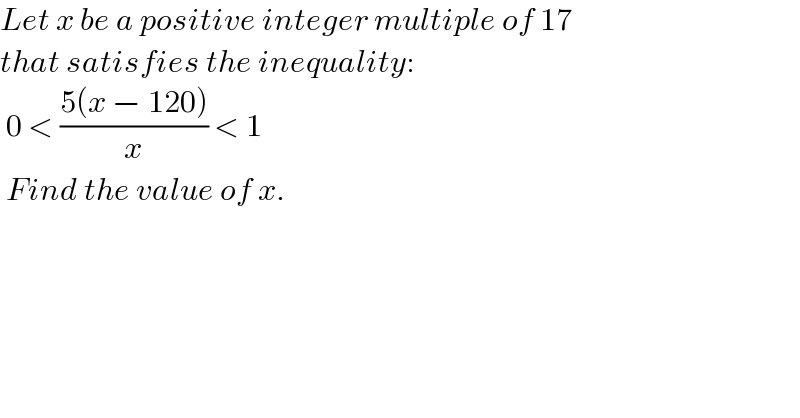
$${Let}\:{x}\:{be}\:{a}\:{positive}\:{integer}\:{multiple}\:{of}\:\mathrm{17} \\ $$ $${that}\:{satisfies}\:{the}\:{inequality}: \\ $$ $$\:\mathrm{0}\:<\:\frac{\mathrm{5}\left({x}\:−\:\mathrm{120}\right)}{{x}}\:<\:\mathrm{1} \\ $$ $$\:{Find}\:{the}\:{value}\:{of}\:{x}. \\ $$
Answered by mr W last updated on 09/Dec/22
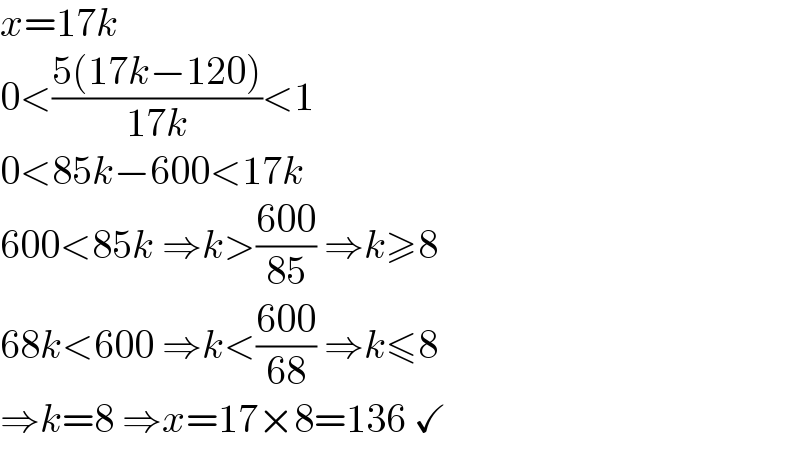
$${x}=\mathrm{17}{k} \\ $$ $$\mathrm{0}<\frac{\mathrm{5}\left(\mathrm{17}{k}−\mathrm{120}\right)}{\mathrm{17}{k}}<\mathrm{1} \\ $$ $$\mathrm{0}<\mathrm{85}{k}−\mathrm{600}<\mathrm{17}{k} \\ $$ $$\mathrm{600}<\mathrm{85}{k}\:\Rightarrow{k}>\frac{\mathrm{600}}{\mathrm{85}}\:\Rightarrow{k}\geqslant\mathrm{8} \\ $$ $$\mathrm{68}{k}<\mathrm{600}\:\Rightarrow{k}<\frac{\mathrm{600}}{\mathrm{68}}\:\Rightarrow{k}\leqslant\mathrm{8} \\ $$ $$\Rightarrow{k}=\mathrm{8}\:\Rightarrow{x}=\mathrm{17}×\mathrm{8}=\mathrm{136}\:\checkmark \\ $$
Answered by MJS_new last updated on 09/Dec/22
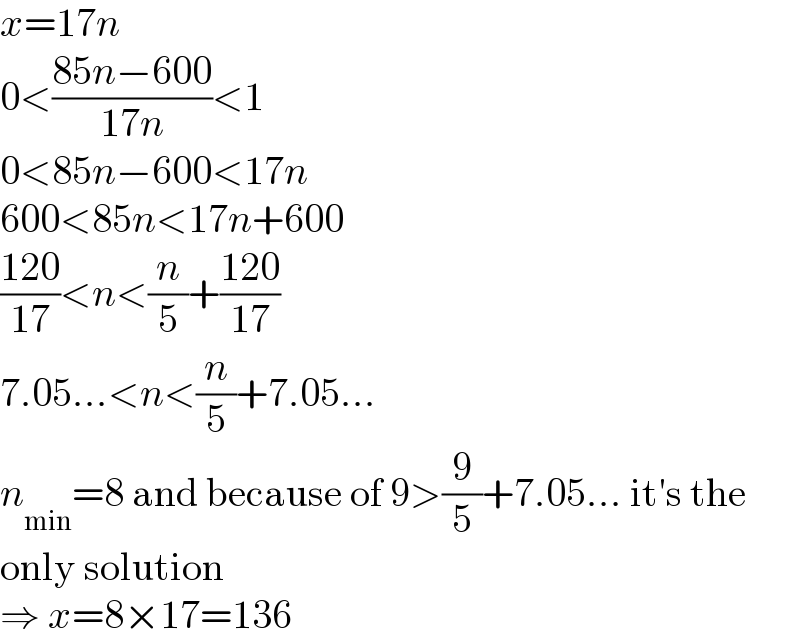
$${x}=\mathrm{17}{n} \\ $$ $$\mathrm{0}<\frac{\mathrm{85}{n}−\mathrm{600}}{\mathrm{17}{n}}<\mathrm{1} \\ $$ $$\mathrm{0}<\mathrm{85}{n}−\mathrm{600}<\mathrm{17}{n} \\ $$ $$\mathrm{600}<\mathrm{85}{n}<\mathrm{17}{n}+\mathrm{600} \\ $$ $$\frac{\mathrm{120}}{\mathrm{17}}<{n}<\frac{{n}}{\mathrm{5}}+\frac{\mathrm{120}}{\mathrm{17}} \\ $$ $$\mathrm{7}.\mathrm{05}...<{n}<\frac{{n}}{\mathrm{5}}+\mathrm{7}.\mathrm{05}... \\ $$ $${n}_{\mathrm{min}} =\mathrm{8}\:\mathrm{and}\:\mathrm{because}\:\mathrm{of}\:\mathrm{9}>\frac{\mathrm{9}}{\mathrm{5}}+\mathrm{7}.\mathrm{05}...\:\mathrm{it}'\mathrm{s}\:\mathrm{the} \\ $$ $$\mathrm{only}\:\mathrm{solution} \\ $$ $$\Rightarrow\:{x}=\mathrm{8}×\mathrm{17}=\mathrm{136} \\ $$
