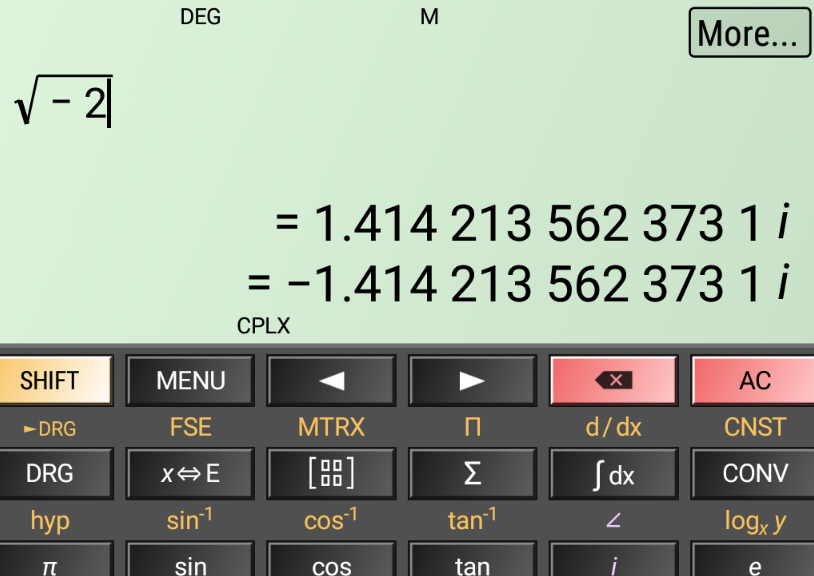
Question Number 182459 by HeferH last updated on 09/Dec/22
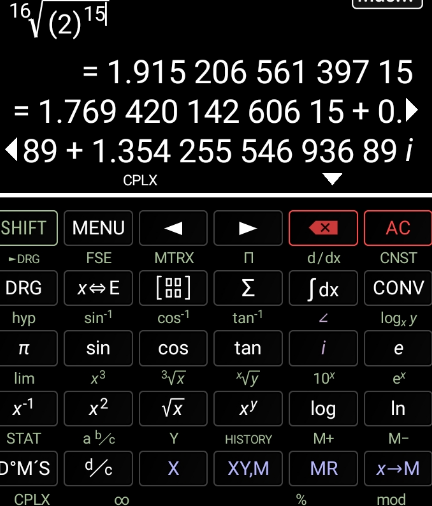
Commented by HeferH last updated on 09/Dec/22
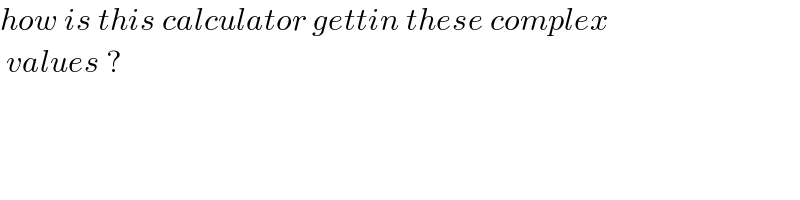
$${how}\:{is}\:{this}\:{calculator}\:{gettin}\:{these}\:{complex} \\ $$$$\:{values}\:? \\ $$
Commented by MJS_new last updated on 09/Dec/22
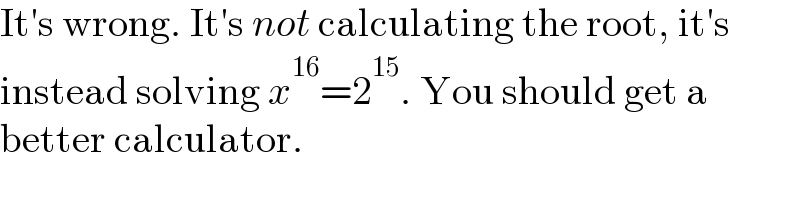
$$\mathrm{It}'\mathrm{s}\:\mathrm{wrong}.\:\mathrm{It}'\mathrm{s}\:{not}\:\mathrm{calculating}\:\mathrm{the}\:\mathrm{root},\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{instead}\:\mathrm{solving}\:{x}^{\mathrm{16}} =\mathrm{2}^{\mathrm{15}} .\:\mathrm{You}\:\mathrm{should}\:\mathrm{get}\:\mathrm{a} \\ $$$$\mathrm{better}\:\mathrm{calculator}. \\ $$
Commented by Acem last updated on 10/Dec/22
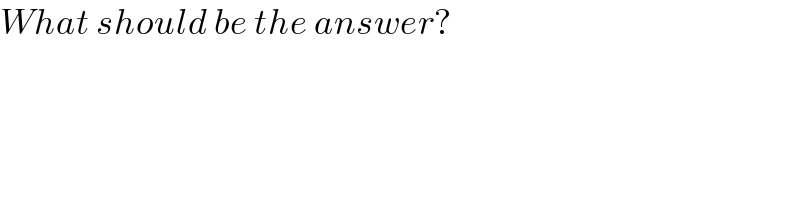
$${What}\:{should}\:{be}\:{the}\:{answer}? \\ $$
Commented by MJS_new last updated on 10/Dec/22
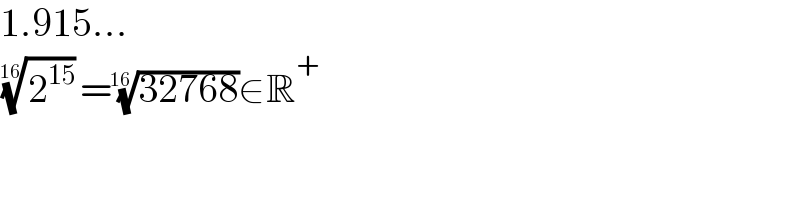
$$\mathrm{1}.\mathrm{915}... \\ $$$$\sqrt[{\mathrm{16}}]{\mathrm{2}^{\mathrm{15}} }=\sqrt[{\mathrm{16}}]{\mathrm{32768}}\in\mathbb{R}^{+} \\ $$
Commented by Acem last updated on 10/Dec/22
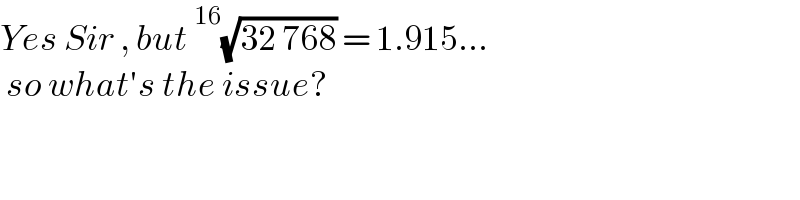
$${Yes}\:{Sir}\:,\:{but}\:^{\mathrm{16}} \sqrt{\mathrm{32}\:\mathrm{768}}\:=\:\mathrm{1}.\mathrm{915}... \\ $$$$\:{so}\:{what}'{s}\:{the}\:{issue}? \\ $$
Commented by Acem last updated on 10/Dec/22

Commented by Acem last updated on 10/Dec/22
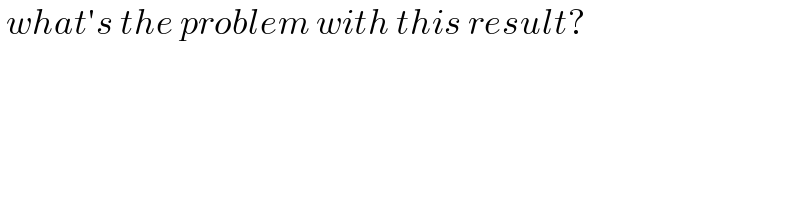
$$\:{what}'{s}\:{the}\:{problem}\:{with}\:{this}\:{result}? \\ $$
Commented by MJS_new last updated on 10/Dec/22

$$\mathrm{no}\:\mathrm{problem}\:\mathrm{with}\:{this}\:\mathrm{result},\:\mathrm{but}\:\mathrm{the}\:\mathrm{calculator} \\ $$$$\mathrm{shows}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{solution}\:\mathrm{too}\:\mathrm{which}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by mr W last updated on 10/Dec/22

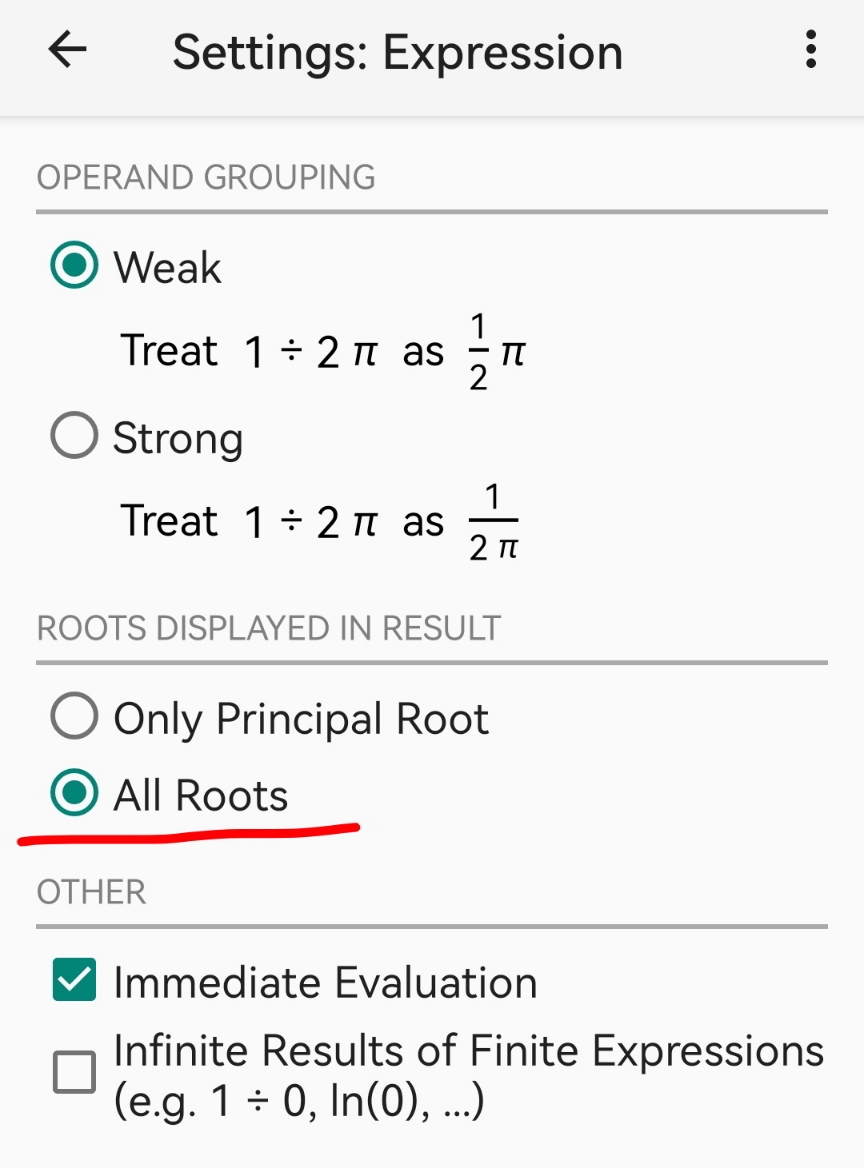
$${this}\:{is}\:{not}\:{a}\:{problem}\:{of}\:{the}\:{app}. \\ $$$${it}\:{displays}\:{all}\:{roots},\:{because}\:{in}\:{this} \\ $$$${case}\:{the}\:{user}\:{has}\:{chosen}\:{to}\:{let}\:{it} \\ $$$${display}\:{all}\:{roots}\:{in}\:{complex}\:{mode}. \\ $$$${if}\:{this}\:{information}\:{confuses}\:{you}, \\ $$$${you}\:{should}\:{not}\:{let}\:{the}\:{app}\:{to}\:{display} \\ $$$${it}.\:{in}\:{settings}\:{you}\:{only}\:{need}\:{to}\:{select} \\ $$$$``{Only}\:{Principal}\:{Root}''\:{instead}\:{of} \\ $$$$``{All}\:{Roots}''. \\ $$
Commented by mr W last updated on 10/Dec/22
Commented by mr W last updated on 10/Dec/22
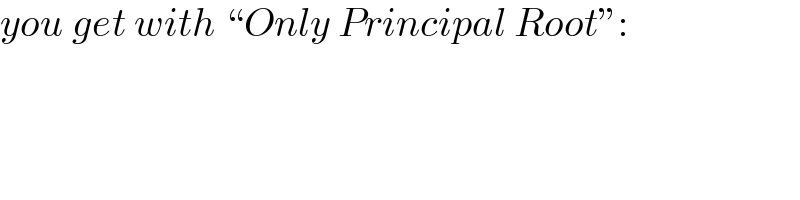
$${you}\:{get}\:{with}\:``{Only}\:{Principal}\:{Root}'': \\ $$
Commented by mr W last updated on 10/Dec/22
Commented by mr W last updated on 10/Dec/22

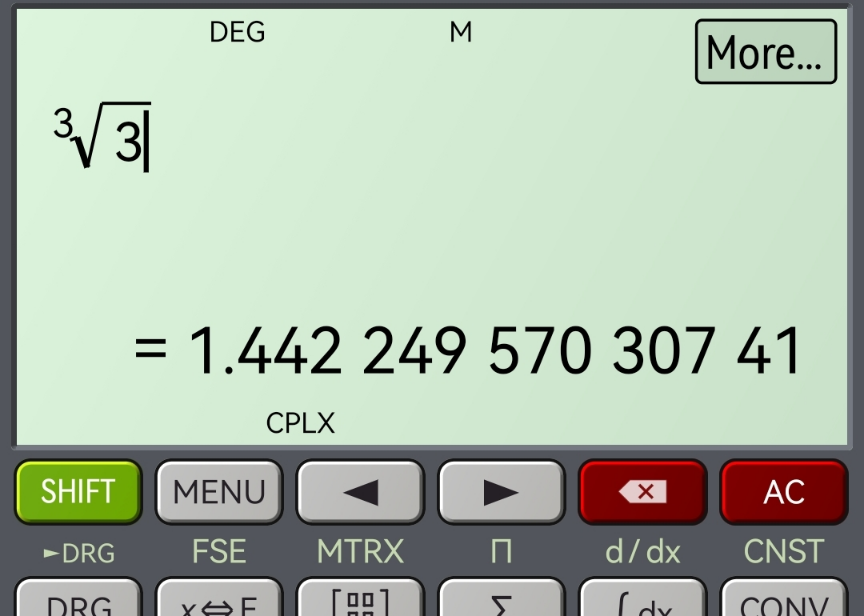
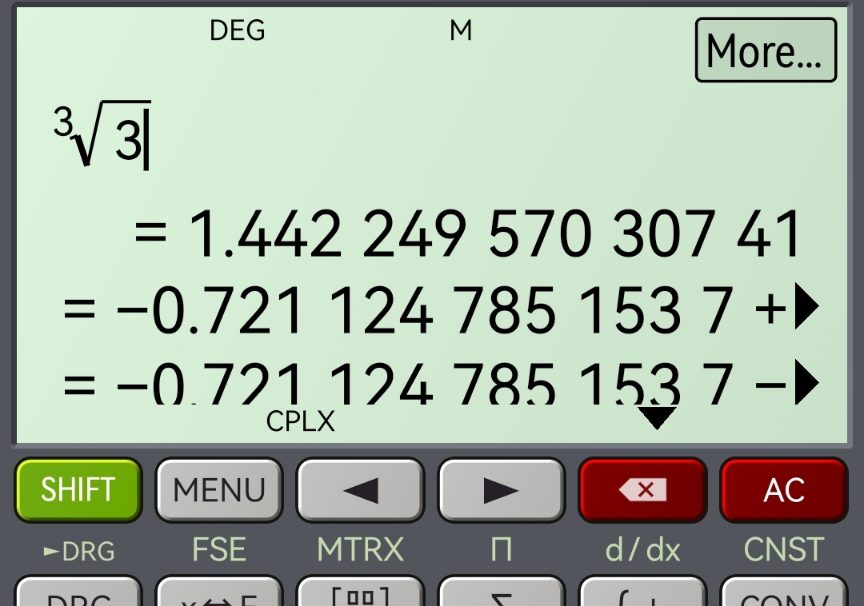
$${you}\:{get}\:{with}\:``{All}\:{Roots}'': \\ $$
Commented by mr W last updated on 10/Dec/22
Commented by mr W last updated on 10/Dec/22

$${by}\:{default}\:{the}\:{app}\:{doesn}'{t}\:{use}\: \\ $$$${complex}\:{mode}\:{and}\:{doesn}'{t}\:{display} \\ $$$${all}\:{roots}.\:{so}\:{i}\:{don}'{t}\:{understand} \\ $$$${those}\:{people}\:{who}\:{explicitly}\:{want}\:{the}\: \\ $$$${app}\:{use}\:{complex}\:{mode}\:{and}\:{display}\: \\ $$$${all}\:{roots},\:{and}\:{then}\:{are}\:{confused}\:{when} \\ $$$${the}\:{app}\:{indeed}\:{does}\:{this}. \\ $$
Commented by MJS_new last updated on 10/Dec/22

$$\mathrm{I}\:\mathrm{hereby}\:\mathrm{give}\:\mathrm{up}. \\ $$$$\mathrm{people}\:\mathrm{started}\:\mathrm{to}\:\mathrm{mix}\:\mathrm{up}\:{x}=\sqrt{\mathrm{4}}\:\mathrm{and}\:{x}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{the}\:\mathrm{app}\:\mathrm{makers}\:\mathrm{also}\:\mathrm{do}\:\mathrm{this}.\:\mathrm{use}\:\mathrm{it} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{like},\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{against}\:\mathrm{the}\:\mathrm{definitions}. \\ $$$$\mathrm{if}\:\sqrt[{\mathrm{16}}]{\mathrm{2}^{\mathrm{15}} }\:\notin\mathbb{R}\:\mathrm{then}\:\mathrm{you}\:\mathrm{also}\:\mathrm{have}\:\mathrm{to}\:\mathrm{accept} \\ $$$$\sqrt{\mathrm{4}}=−\mathrm{2}\:\mathrm{with}\:\mathrm{all}\:\mathrm{kinds}\:\mathrm{of}\:\mathrm{weird}\:\mathrm{logical} \\ $$$$\mathrm{problems}. \\ $$$$\mathrm{i}.\mathrm{e}.\:\mid{z}\mid\geqslant\mathrm{0}\forall{z}\in\mathbb{C}\:\mathrm{and}\:\mid{a}+{b}\mathrm{i}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\mathrm{but}\:\mathrm{what}\:\mathrm{if}\:{z}=\sqrt[{\mathrm{4}}]{\mathrm{16}}+\sqrt[{\mathrm{4}}]{\mathrm{81}}\mathrm{i}?\:\mathrm{how}\:\mathrm{many}\:\mathrm{values} \\ $$$$\mathrm{is}\:{z}\:\mathrm{at}\:\mathrm{once}\:\mathrm{or}\:\mathrm{which}\:\mathrm{value}\:\mathrm{is}\:\mathrm{the}\:``\mathrm{main}\:\mathrm{value}''? \\ $$$$\mathrm{and}\:\sqrt{\left(\sqrt[{\mathrm{4}}]{\mathrm{16}}\right)^{\mathrm{2}} +\left(\sqrt[{\mathrm{4}}]{\mathrm{81}}\right)^{\mathrm{2}} }\:\mathrm{can}\:\mathrm{not}\:\mathrm{only}\:\mathrm{be}\:<\mathrm{0}\:\mathrm{but} \\ $$$$\mathrm{also}\:\mathrm{be}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number}??? \\ $$$$\mathrm{or}\:\mathrm{simply}: \\ $$$$\sqrt{\mathrm{4}}+\sqrt{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{proof}: \\ $$$$\sqrt{\mathrm{4}}=−\mathrm{2}\vee\sqrt{\mathrm{4}}=\mathrm{2} \\ $$$$\Rightarrow\:\sqrt{\mathrm{4}}+\sqrt{\mathrm{4}}=−\mathrm{2}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{I}'\mathrm{ll}\:\mathrm{keep}\:\mathrm{following}\:\mathrm{the}\:\mathrm{rules}\:\mathrm{I}\:\mathrm{learned}\:\mathrm{35}\:\mathrm{years} \\ $$$$\mathrm{ago},\:\mathrm{everybody}\:\mathrm{else}\:\mathrm{is}\:\mathrm{free}\:\mathrm{to}\:\mathrm{use}\:\mathrm{whatever} \\ $$$$\mathrm{they}\:\mathrm{want}. \\ $$
Commented by MJS_new last updated on 10/Dec/22

$$\mathrm{if}\:\mathrm{these}\:``\mathrm{new}\:\mathrm{rules}''\:\mathrm{are}\:\mathrm{used} \\ $$$$\sqrt[{\mathrm{4}}]{{x}+\mathrm{3}}−\sqrt{{x}+\mathrm{4}}=\mathrm{3} \\ $$$$\mathrm{has}\:\mathrm{2}\:\mathrm{solutions}: \\ $$$${x}_{\mathrm{1}} \approx−.\mathrm{816094359} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{23}.\mathrm{8367388} \\ $$$$\mathrm{someone}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{opposite}... \\ $$
Commented by mr W last updated on 10/Dec/22

$${i}\:{totally}\:{agree}\:{with}\:{sir}!\:{basically}\:{it} \\ $$$${is}\:{clear}\:{and}\:\mathrm{100\%}\:{correct}\:{what}\:{you}\: \\ $$$${said}. \\ $$$${but}\:{as}\:{about}\:{the}\:{app},\:{i}\:{don}'{t}\:{think}\:{that} \\ $$$${the}\:{app}\:{makes}\:{an}\:{error}.\:{it}\:{states} \\ $$$${clearly}\:{that}\:{it}\:{displays}\:{all}\:{roots}\:{of} \\ $$$${a}\:{number}\:{in}\:{complex}\:{plane}. \\ $$$${in}\:{complex}\:{mode}\:{this}\:{app}\:{means}\: \\ $$$${with}\:\sqrt[{\mathrm{3}}]{\mathrm{3}}\:{simply}\:{the}\:{roots}\:{of}\:{the}\:{number} \\ $$$$\mathrm{3}\:{in}\:{complex}\:{plane}. \\ $$
Commented by Acem last updated on 10/Dec/22

$${Yes}\:{I}\:{agree}\:{with}\:{you}\:{Sir}\:{MJS} \\ $$
Commented by Acem last updated on 10/Dec/22

$${The}\:{wrong}\:{is}\:{not}\:{with}\:{the}\:{application}\:{but}\:{with} \\ $$$$\:{how}\:{it}\:{is}\:{used}.\:{The}\:{option}\:{CPLX}\:{must}\:{chosen}\:{just} \\ $$$$\:{for}\:\mathbb{R}^{\:−} \: \\ $$
Commented by Acem last updated on 10/Dec/22