
Question Number 182367 by universe last updated on 08/Dec/22
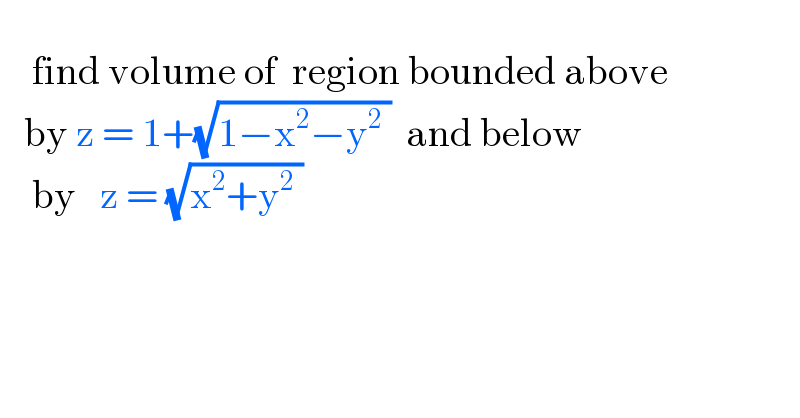
$$ \\ $$$$\:\:\:\:\mathrm{find}\:\mathrm{volume}\:\mathrm{of}\:\:\mathrm{region}\:\mathrm{bounded}\:\mathrm{above}\: \\ $$$$\:\:\:\mathrm{by}\:\mathrm{z}\:=\:\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \:}\:\:\mathrm{and}\:\mathrm{below} \\ $$$$\:\:\:\:\mathrm{by}\:\:\:\mathrm{z}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:}\: \\ $$
Answered by Tokugami last updated on 08/Dec/22
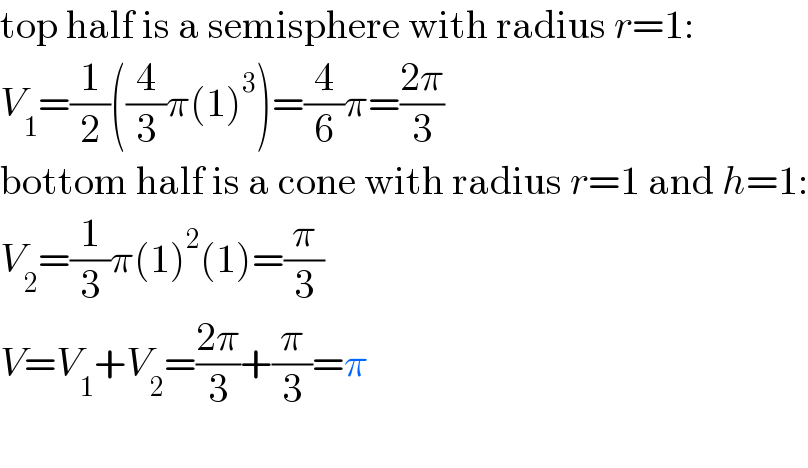
$$\mathrm{top}\:\mathrm{half}\:\mathrm{is}\:\mathrm{a}\:\mathrm{semisphere}\:\mathrm{with}\:\mathrm{radius}\:{r}=\mathrm{1}: \\ $$$${V}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{3}}\pi\left(\mathrm{1}\right)^{\mathrm{3}} \right)=\frac{\mathrm{4}}{\mathrm{6}}\pi=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{bottom}\:\mathrm{half}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cone}\:\mathrm{with}\:\mathrm{radius}\:{r}=\mathrm{1}\:\mathrm{and}\:{h}=\mathrm{1}: \\ $$$${V}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}\pi\left(\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{3}} \\ $$$${V}={V}_{\mathrm{1}} +{V}_{\mathrm{2}} =\frac{\mathrm{2}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{3}}=\pi \\ $$$$ \\ $$
