
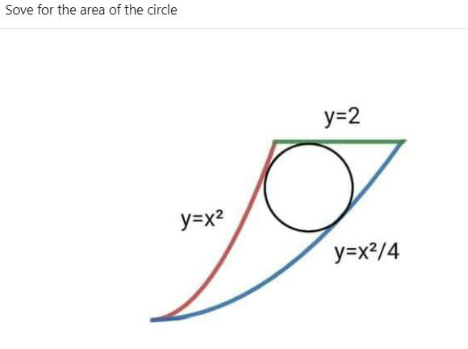
Question Number 182298 by SEKRET last updated on 07/Dec/22
Answered by mr W last updated on 07/Dec/22

$${radius}:\:{r} \\ $$$${center}:\:\left({k},\mathrm{2}−{r}\right) \\ $$$${touching}\:{point}\:{with}\:{y}={x}^{\mathrm{2}} :\:\left({p},{p}^{\mathrm{2}} \right) \\ $$$${touching}\:{point}\:{with}\:{y}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}:\:\left({q},\frac{{q}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$${k}={p}+{r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{k}={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\mathrm{2}−{r}={p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{2}−{r}={p}^{\mathrm{2}} −\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\varphi=\frac{{q}}{\mathrm{2}} \\ $$$${k}={q}−{r}\:\mathrm{sin}\:\varphi \\ $$$$\Rightarrow{k}={q}−\frac{{qr}}{\:\sqrt{\mathrm{4}+{q}^{\mathrm{2}} }} \\ $$$$\mathrm{2}−{r}=\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+{r}\:\mathrm{cos}\:\varphi \\ $$$$\Rightarrow\mathrm{2}−{r}=\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{4}+{q}^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}=\frac{{q}−{p}}{\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}+\frac{{q}}{\:\sqrt{\mathrm{4}+{q}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}−{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}−\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{q}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{p}\approx\mathrm{1}.\mathrm{29415},\:{q}\approx\mathrm{2}.\mathrm{13965} \\ $$$$\Rightarrow{r}\approx\mathrm{0}.\mathrm{5084} \\ $$
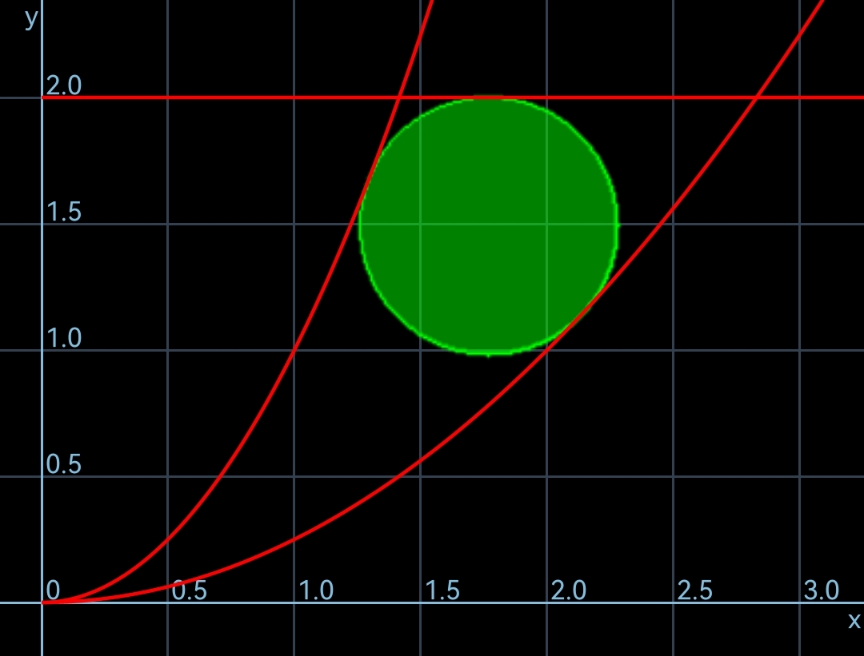
Commented by mr W last updated on 07/Dec/22
Commented by SEKRET last updated on 07/Dec/22

$$\:\boldsymbol{\mathrm{thank}}\:\:\boldsymbol{\mathrm{you}}\: \\ $$
