
Question Number 182292 by HeferH last updated on 07/Dec/22
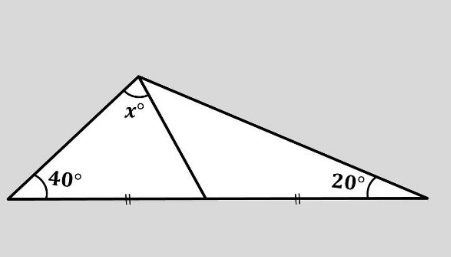
Answered by Acem last updated on 07/Dec/22
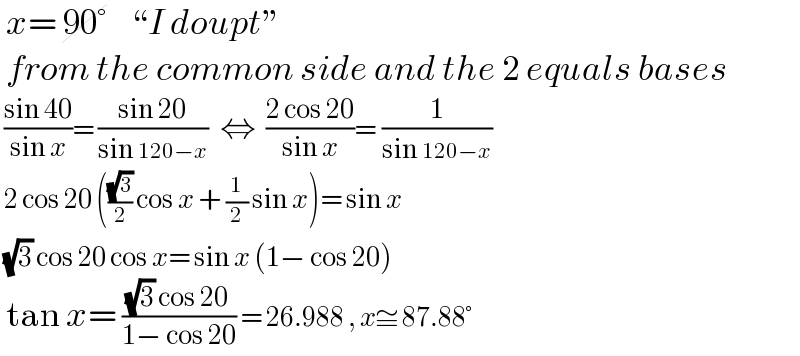
$$\:{x}=\:\cancel{\mathrm{90}°}\:\:\:\:``{I}\:{doupt}'' \\ $$$$\:{from}\:{the}\:{common}\:{side}\:{and}\:{the}\:\mathrm{2}\:{equals}\:{bases} \\ $$$$\:\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:{x}}=\:\frac{\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{120}−{x}}\:\:\Leftrightarrow\:\:\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{20}}{\mathrm{sin}\:{x}}=\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{120}−{x}} \\ $$$$\:\mathrm{2}\:\mathrm{cos}\:\mathrm{20}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:{x}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:{x}\right)=\:\mathrm{sin}\:{x} \\ $$$$\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{20}\:\mathrm{cos}\:{x}=\:\mathrm{sin}\:{x}\:\left(\mathrm{1}−\:\mathrm{cos}\:\mathrm{20}\right) \\ $$$$\:\mathrm{tan}\:{x}=\:\frac{\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{20}}{\mathrm{1}−\:\mathrm{cos}\:\mathrm{20}}\:=\:\mathrm{26}.\mathrm{988}\:,\:{x}\cong\:\mathrm{87}.\mathrm{88}° \\ $$
Commented by HeferH last updated on 07/Dec/22

$$\left.{I}\:{would}\:{like}\:{to}\:{see}\:{the}\:{process}\::\right) \\ $$$$ \\ $$
Commented by Acem last updated on 07/Dec/22

$$\left.{Haha},\:{i}\:{did}\:{like}\:{you}\:{last}\:{time}\::\right) \\ $$$${in}\:{fact}\:{by}\:{laws}\:{it}'{s}\:{very}\:{easy},\:{but}\:{i}\:{would}\:{to}\:{do} \\ $$$${it}\:{by}\:{Euclidean}\:{method}.\:{I}\:{did},\:{but}\:{it}\:{was}\:{very} \\ $$$$\:{complicated},\:{so}\:{please}\:{give}\:{me}\:{time}\:{to}\:{find}\:{another} \\ $$$$\:{simpler}\:{way}.\:{Thanks}\:{for}\:{this}\:{question}\:\left(:\right. \\ $$
Commented by Acem last updated on 07/Dec/22
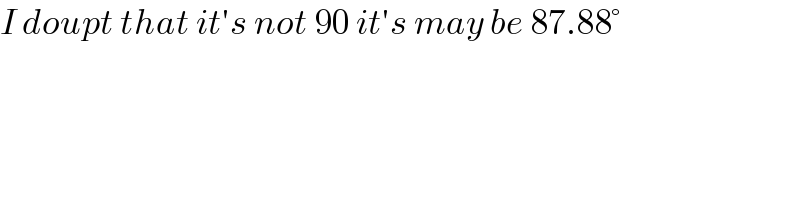
$${I}\:{doupt}\:{that}\:{it}'{s}\:{not}\:\mathrm{90}\:{it}'{s}\:{may}\:{be}\:\mathrm{87}.\mathrm{88}° \\ $$
Commented by Acem last updated on 07/Dec/22

$${When}\:{i}\:{solved}\:{it}\:{with}\:{Euclidean}\:{method}, \\ $$$$\:``{was}\:{complicated}''{i}\:{wasn}'{t}\:{know}\:{that}\:{i}\:{had}\: \\ $$$$\:{a}\:{mistake}\:{in}\:{one}\:{of}\:{assumptions},\:{comparing}\:{it} \\ $$$$\:{with}\:{using}\:{laws}\:{i}\:{got}\:{less}\:{than}\:\mathrm{90},\:{that}\:{made} \\ $$$$\:{me}\:{doupt}\:{that}\:{i}\:{have}\:{some}\:{wrong}\:{in}\:{formulas} \\ $$$$\:{thought}\:{it}\:{was}\:{correct}!\:{when}\:{i}\:{try}\:{it}\:{again}\:{with} \\ $$$$\:{Euclidean}\:{method}\:{i}\:{knew}\:{that}\:{i}\:{have}\:{a}\:{mistake}. \\ $$$$ \\ $$$$\:{However}\:{i}\:{will}\:{not}\:{hate}\:{that}\:{method},\:{sometimes} \\ $$$$\:{give}\:{me}\:{the}\:{solution}\:{as}\:{faster},\:{plus}\:{it}'{s}\: \\ $$$$\:{more}\:{fun}.\: \\ $$
Answered by SEKRET last updated on 04/Jan/23
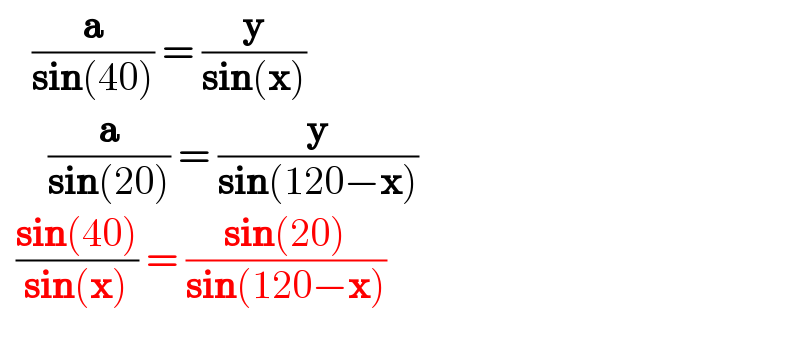
$$\:\:\:\:\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{sin}}\left(\mathrm{40}\right)}\:=\:\frac{\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)} \\ $$$$\:\:\:\:\:\:\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{sin}}\left(\mathrm{20}\right)}\:=\:\frac{\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{sin}}\left(\mathrm{120}−\boldsymbol{\mathrm{x}}\right)} \\ $$$$\:\:\frac{\boldsymbol{\mathrm{sin}}\left(\mathrm{40}\right)}{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}\:=\:\frac{\boldsymbol{\mathrm{sin}}\left(\mathrm{20}\right)}{\boldsymbol{\mathrm{sin}}\left(\mathrm{120}−\boldsymbol{\mathrm{x}}\right)} \\ $$$$ \\ $$
Commented by Acem last updated on 07/Dec/22
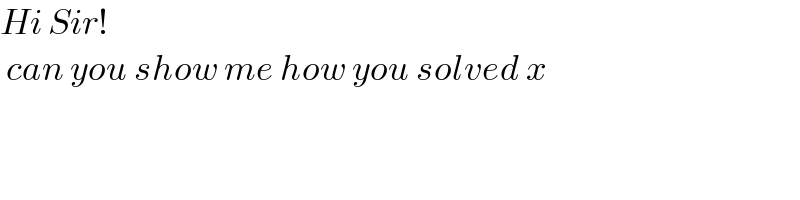
$${Hi}\:{Sir}! \\ $$$$\:{can}\:{you}\:{show}\:{me}\:{how}\:{you}\:{solved}\:{x} \\ $$
Commented by Acem last updated on 07/Dec/22
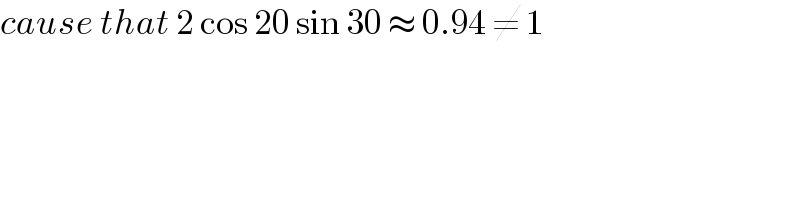
$${cause}\:{that}\:\mathrm{2}\:\mathrm{cos}\:\mathrm{20}\:\mathrm{sin}\:\mathrm{30}\:\approx\:\mathrm{0}.\mathrm{94}\:\neq\:\mathrm{1} \\ $$
Answered by mr W last updated on 07/Dec/22
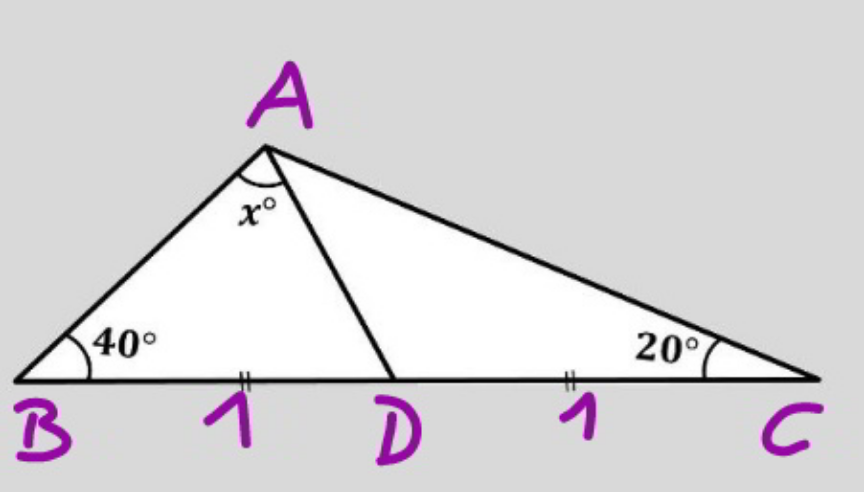
Commented by mr W last updated on 07/Dec/22
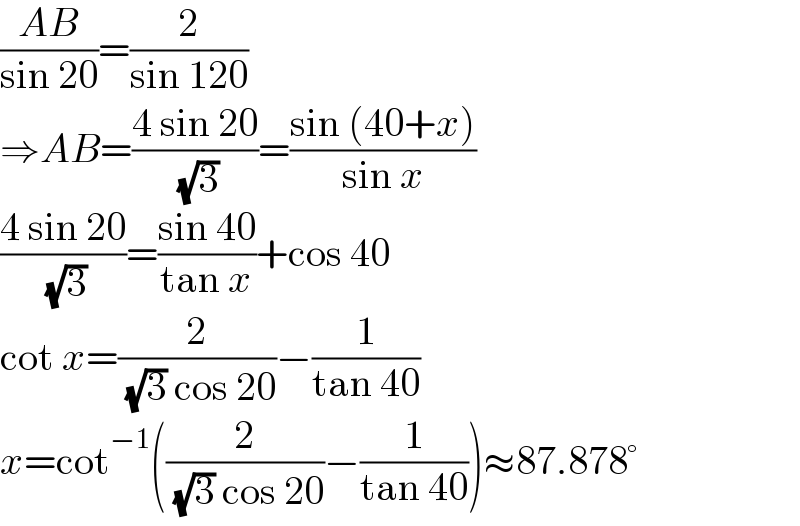
$$\frac{{AB}}{\mathrm{sin}\:\mathrm{20}}=\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{120}} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{20}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{sin}\:\left(\mathrm{40}+{x}\right)}{\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{20}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{tan}\:{x}}+\mathrm{cos}\:\mathrm{40} \\ $$$$\mathrm{cot}\:{x}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{20}}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{40}} \\ $$$${x}=\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{20}}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{40}}\right)\approx\mathrm{87}.\mathrm{878}° \\ $$
Commented by Acem last updated on 07/Dec/22
$${Exactly}!\:{as}\:{i}\:{recently}\:{got} \\ $$
