
Question Number 182199 by depressiveshrek last updated on 05/Dec/22

$${Let}\:{S}=\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6},\:\mathrm{7}\right\} \\ $$$${If}\:{we}\:{multiply}\:{atleast}\:\mathrm{2}\:{numbers} \\ $$$${from}\:{this}\:{set}\:{with}\:{each}\:{other},\:{what} \\ $$$${are}\:{the}\:{chances}\:{of}\:{the}\:{product}\:{to} \\ $$$${turn}\:{out}\:{to}\:{be}\:{divisible}\:{by}\:\mathrm{3}? \\ $$
Answered by Acem last updated on 06/Dec/22

$$\:{This}\:{solution}\:{is}\:{for}\:{product}\:{only}\:\mathrm{2}\:{numbers} \\ $$$$\:{I}\:{will}\:{solve}\:{the}\:{question}\:{later} \\ $$$$\:{P}\left({product}_{{div}.\:{by}\:\mathrm{3}} \right)=\:\frac{\mathrm{11}}{\mathrm{21}}\: \\ $$$$\:{a}×{b},\:{b}×{a}\:\equiv\:{one}\:{way}, \\ $$$$\:{a}×{a}\:{is}\:{refused}\:{according}\:\:{to}\:{the}\:{question} \\ $$$$ \\ $$$$\:{The}\:{method}: \\ $$$$\:{S}_{\mathrm{1}} =\:\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:\mathrm{5},\:\mathrm{7}\right\}\:\:\:\:,\:\:{S}_{\mathrm{2}} =\:\left\{\mathrm{3},\:\mathrm{6}\right\} \\ $$$$ \\ $$$$\:\:{P}\left({product}_{{div}.\:{by}\:\mathrm{3}} \right)=\:\frac{{C}_{\mathrm{1}} ^{\:\mathrm{5}} \:{C}_{\:\mathrm{1}} ^{\:\mathrm{2}} \:+\:\underset{{S}_{\mathrm{2}} } {\underbrace{{C}_{\:\mathrm{2}} ^{\:\mathrm{2}} }}}{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}}\:\:\:\:\:\:\:\:\:\:;\:{n}=\:\mathrm{7} \\ $$
Commented by mr W last updated on 06/Dec/22

$${the}\:{question}\:{is}\:``{take}\:{at}\:{least}\:{two}\: \\ $$$${numbers}'',\:{not}\:``{take}\:{only}\:{two}\: \\ $$$${numbers}''\:{as}\:{you}\:{assumed}. \\ $$
Commented by Acem last updated on 06/Dec/22
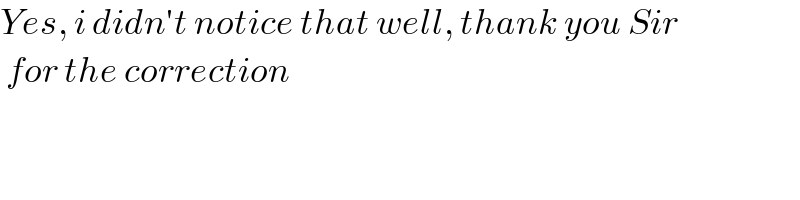
$${Yes},\:{i}\:{didn}'{t}\:{notice}\:{that}\:{well},\:{thank}\:{you}\:{Sir} \\ $$$$\:{for}\:{the}\:{correction} \\ $$
Answered by mr W last updated on 06/Dec/22

$$\left.\mathrm{1}\right)\:{take}\:\mathrm{7}\:{numbers} \\ $$$${total}:\:\mathrm{1}\:{way} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{1}\:{way} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{take}\:\mathrm{6}\:{numbers} \\ $$$${total}:\:\mathrm{7}\:{ways} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{7}\:{ways} \\ $$$$ \\ $$$$\left.\mathrm{3}\right)\:{take}\:\mathrm{5}\:{numbers} \\ $$$${total}:\:{C}_{\mathrm{5}} ^{\mathrm{7}} =\mathrm{21}\:{ways} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{1}×{C}_{\mathrm{3}} ^{\mathrm{5}} +\mathrm{2}×{C}_{\mathrm{4}} ^{\mathrm{5}} =\mathrm{20} \\ $$$$ \\ $$$$\left.\mathrm{4}\right)\:{take}\:\mathrm{4}\:{numbers} \\ $$$${total}:\:{C}_{\mathrm{4}} ^{\mathrm{7}} =\mathrm{35}\:{ways} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{1}×{C}_{\mathrm{2}} ^{\mathrm{5}} +\mathrm{2}×{C}_{\mathrm{3}} ^{\mathrm{5}} =\mathrm{30} \\ $$$$ \\ $$$$\left.\mathrm{5}\right)\:{take}\:\mathrm{3}\:{numbers} \\ $$$${total}:\:{C}_{\mathrm{3}} ^{\mathrm{7}} =\mathrm{35}\:{ways} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{1}×{C}_{\mathrm{1}} ^{\mathrm{5}} +\mathrm{2}×{C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{25} \\ $$$$ \\ $$$$\left.\mathrm{6}\right)\:{take}\:\mathrm{2}\:{numbers} \\ $$$${total}:\:{C}_{\mathrm{2}} ^{\mathrm{7}} =\mathrm{21}\:{ways} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{1}+\mathrm{2}×{C}_{\mathrm{1}} ^{\mathrm{5}} =\mathrm{11} \\ $$$$ \\ $$$$\boldsymbol{{take}}\:\boldsymbol{{at}}\:\boldsymbol{{least}}\:\mathrm{2}\:\boldsymbol{{numbers}}: \\ $$$${total}:\:\mathrm{1}+\mathrm{7}+\mathrm{21}+\mathrm{35}+\mathrm{35}+\mathrm{21}=\mathrm{120}\:{ways} \\ $$$${divisible}\:{by}\:\mathrm{3}:\:\mathrm{1}+\mathrm{7}+\mathrm{20}+\mathrm{30}+\mathrm{25}+\mathrm{11}=\mathrm{94}\:{ways} \\ $$$${p}=\frac{\mathrm{94}}{\mathrm{120}}\approx\mathrm{78}.\mathrm{3\%} \\ $$
