
Question Number 182109 by amin96 last updated on 04/Dec/22
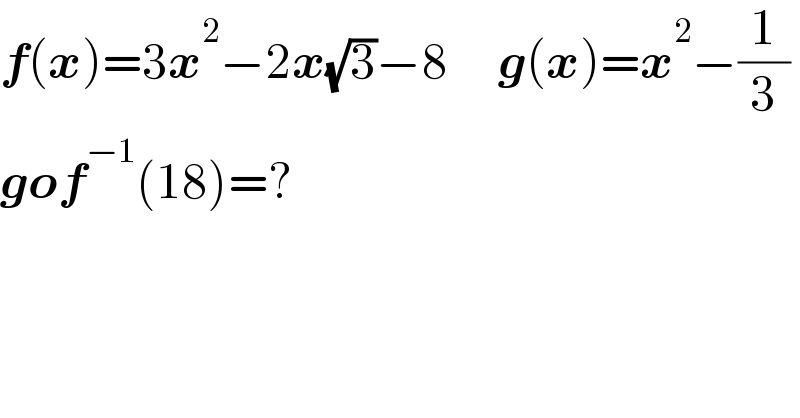
$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\mathrm{3}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}\sqrt{\mathrm{3}}−\mathrm{8}\:\:\:\:\:\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{x}}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\boldsymbol{{gof}}^{−\mathrm{1}} \left(\mathrm{18}\right)=? \\ $$
Answered by FelipeLz last updated on 04/Dec/22
![f(x) = 3x^2 −2x(√3)−8 f(x) = 3x^2 −2(√3)x+1−1−8 f(x) = ((√3)x−1)^2 −9 x = ((√3)f^(−1) (x)−1)^2 −9 f^(−1) (x) = (1/( (√3)))(1+(√(x+9))) g○f^(−1) (x) = [(1/( (√3)))(1+(√(x+9)))]^2 −(1/3) g○f^(−1) (x) = (1/3)(10+2(√(x+9))+x)−(1/3) g○f^(−1) (x) = (1/3)(9+2(√(x+9))+x) g○f^(−1) (18) = (1/3)(27+2(√(27))) g○f^(−1) (18) = (1/3)(27+6(√3)) = 9+2(√3)](Q182112.png)
$${f}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}\sqrt{\mathrm{3}}−\mathrm{8} \\ $$$${f}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{x}+\mathrm{1}−\mathrm{1}−\mathrm{8} \\ $$$${f}\left({x}\right)\:=\:\left(\sqrt{\mathrm{3}}{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{9} \\ $$$${x}\:=\:\left(\sqrt{\mathrm{3}}{f}^{−\mathrm{1}} \left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{9} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\sqrt{{x}+\mathrm{9}}\right) \\ $$$${g}\circ{f}^{−\mathrm{1}} \left({x}\right)\:=\:\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\sqrt{{x}+\mathrm{9}}\right)\right]^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${g}\circ{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{10}+\mathrm{2}\sqrt{{x}+\mathrm{9}}+{x}\right)−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${g}\circ{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{9}+\mathrm{2}\sqrt{{x}+\mathrm{9}}+{x}\right) \\ $$$${g}\circ{f}^{−\mathrm{1}} \left(\mathrm{18}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{27}+\mathrm{2}\sqrt{\mathrm{27}}\right) \\ $$$${g}\circ{f}^{−\mathrm{1}} \left(\mathrm{18}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{27}+\mathrm{6}\sqrt{\mathrm{3}}\right)\:=\:\mathrm{9}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$ \\ $$
