Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 182073 by Acem last updated on 04/Dec/22

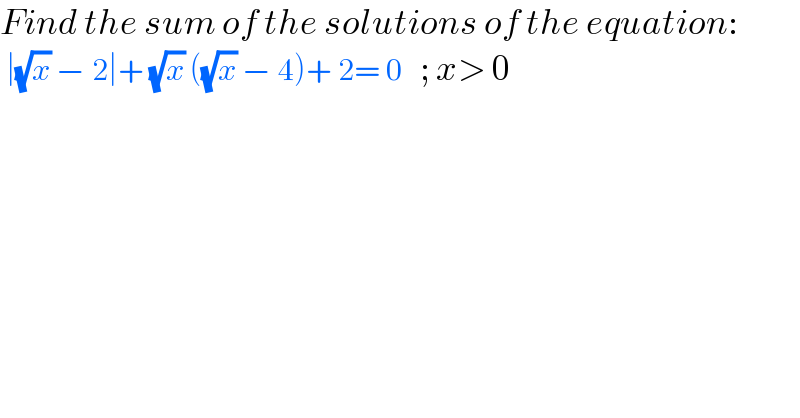
Find the sum of the solutions of the equation: ∣(√x) − 2∣+ (√x) ((√x) − 4)+ 2= 0 ; x> 0

$${Find}\:{the}\:{sum}\:{of}\:{the}\:{solutions}\:{of}\:{the}\:{equation}: \\ $$ $$\:\mid\sqrt{{x}}\:−\:\mathrm{2}\mid+\:\sqrt{{x}}\:\left(\sqrt{{x}}\:−\:\mathrm{4}\right)+\:\mathrm{2}=\:\mathrm{0}\:\:\:;\:{x}>\:\mathrm{0} \\ $$

Answered by HeferH last updated on 04/Dec/22

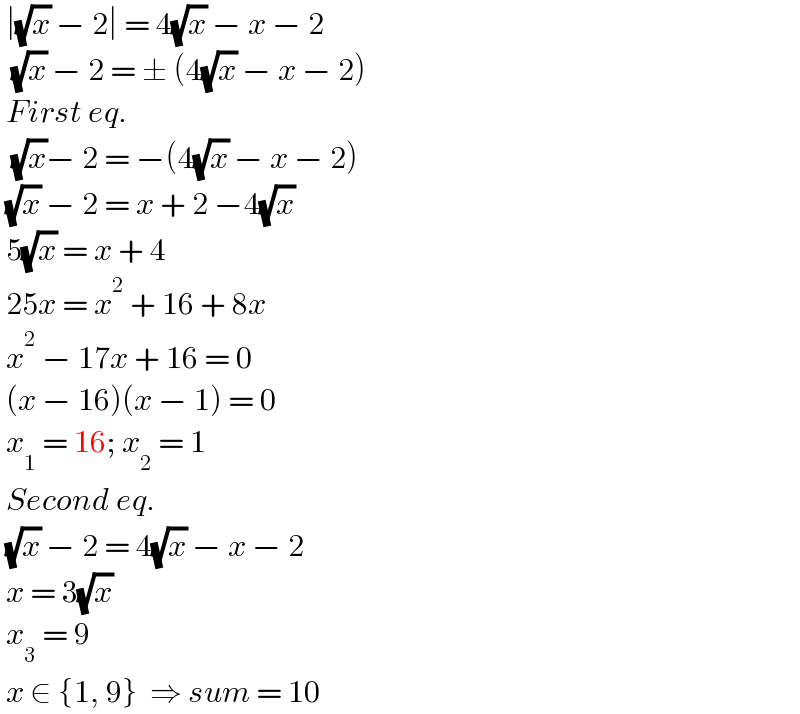
∣(√x) − 2∣ = 4(√x) − x − 2 (√x) − 2 = ± (4(√x) − x − 2) First eq. (√x)− 2 = −(4(√x) − x − 2) (√x) − 2 = x + 2 −4(√x) 5(√x) = x + 4 25x = x^2 + 16 + 8x x^2 − 17x + 16 = 0 (x − 16)(x − 1) = 0 x_1 = 16; x_2 = 1 Second eq. (√x) − 2 = 4(√x) − x − 2 x = 3(√x) x_3 = 9 x ∈ {1, 9} ⇒ sum = 10

$$\:\mid\sqrt{{x}}\:−\:\mathrm{2}\mid\:=\:\mathrm{4}\sqrt{{x}}\:−\:{x}\:−\:\mathrm{2} \\ $$ $$\:\:\sqrt{{x}}\:−\:\mathrm{2}\:=\:\pm\:\left(\mathrm{4}\sqrt{{x}}\:−\:{x}\:−\:\mathrm{2}\right) \\ $$ $$\:{First}\:{eq}. \\ $$ $$\:\:\sqrt{{x}}−\:\mathrm{2}\:=\:−\left(\mathrm{4}\sqrt{{x}}\:−\:{x}\:−\:\mathrm{2}\right) \\ $$ $$\:\sqrt{{x}}\:−\:\mathrm{2}\:=\:{x}\:+\:\mathrm{2}\:−\mathrm{4}\sqrt{{x}} \\ $$ $$\:\mathrm{5}\sqrt{{x}}\:=\:{x}\:+\:\mathrm{4} \\ $$ $$\:\mathrm{25}{x}\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{16}\:+\:\mathrm{8}{x} \\ $$ $$\:{x}^{\mathrm{2}} \:−\:\mathrm{17}{x}\:+\:\mathrm{16}\:=\:\mathrm{0} \\ $$ $$\:\left({x}\:−\:\mathrm{16}\right)\left({x}\:−\:\mathrm{1}\right)\:=\:\mathrm{0} \\ $$ $$\:{x}_{\mathrm{1}} \:=\:\mathrm{16};\:{x}_{\mathrm{2}} \:=\:\mathrm{1} \\ $$ $$\:{Second}\:{eq}. \\ $$ $$\:\sqrt{{x}}\:−\:\mathrm{2}\:=\:\mathrm{4}\sqrt{{x}}\:−\:{x}\:−\:\mathrm{2} \\ $$ $$\:{x}\:=\:\mathrm{3}\sqrt{{x}} \\ $$ $$\:{x}_{\mathrm{3}} \:=\:\mathrm{9}\: \\ $$ $$\:{x}\:\in\:\left\{\mathrm{1},\:\mathrm{9}\right\}\:\:\Rightarrow\:{sum}\:=\:\mathrm{10} \\ $$

Commented bymanxsol last updated on 04/Dec/22

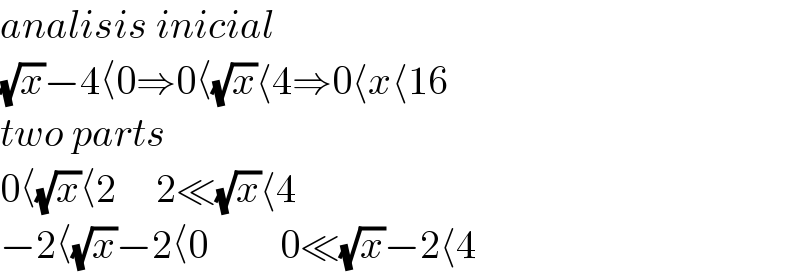
analisis inicial (√x)−4⟨0⇒0⟨(√x)⟨4⇒0⟨x⟨16 two parts 0⟨(√x)⟨2 2≪(√x)⟨4 −2⟨(√x)−2⟨0 0≪(√x)−2⟨4

$${analisis}\:{inicial} \\ $$ $$\sqrt{{x}}−\mathrm{4}\langle\mathrm{0}\Rightarrow\mathrm{0}\langle\sqrt{{x}}\langle\mathrm{4}\Rightarrow\mathrm{0}\langle{x}\langle\mathrm{16} \\ $$ $${two}\:{parts} \\ $$ $$\mathrm{0}\langle\sqrt{{x}}\langle\mathrm{2}\:\:\:\:\:\mathrm{2}\ll\sqrt{{x}}\langle\mathrm{4} \\ $$ $$−\mathrm{2}\langle\sqrt{{x}}−\mathrm{2}\langle\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{0}\ll\sqrt{{x}}−\mathrm{2}\langle\mathrm{4}\:\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com