
Question Number 18184 by Tinkutara last updated on 16/Jul/17
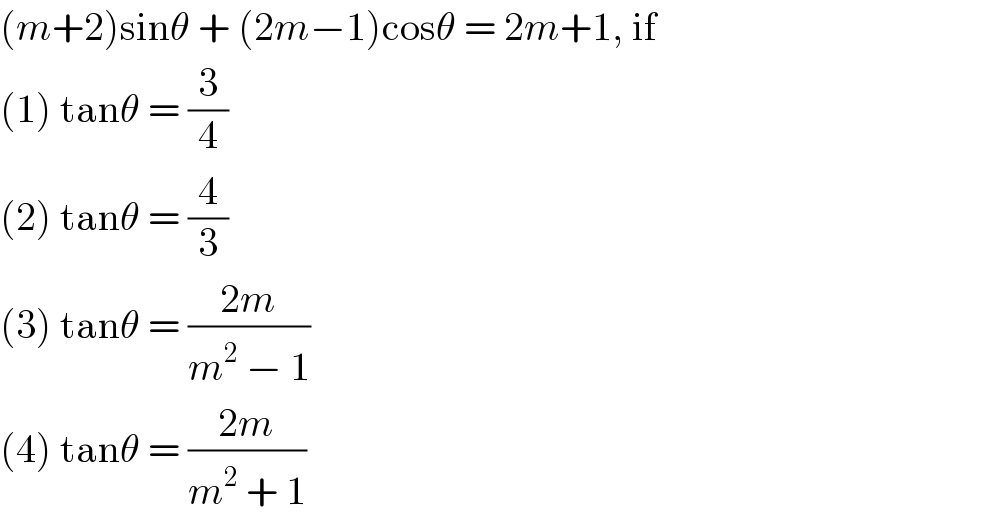
$$\left({m}+\mathrm{2}\right)\mathrm{sin}\theta\:+\:\left(\mathrm{2}{m}−\mathrm{1}\right)\mathrm{cos}\theta\:=\:\mathrm{2}{m}+\mathrm{1},\:\mathrm{if} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{tan}\theta\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{tan}\theta\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{tan}\theta\:=\:\frac{\mathrm{2}{m}}{{m}^{\mathrm{2}} \:−\:\mathrm{1}} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{tan}\theta\:=\:\frac{\mathrm{2}{m}}{{m}^{\mathrm{2}} \:+\:\mathrm{1}} \\ $$
Commented by prakash jain last updated on 16/Jul/17
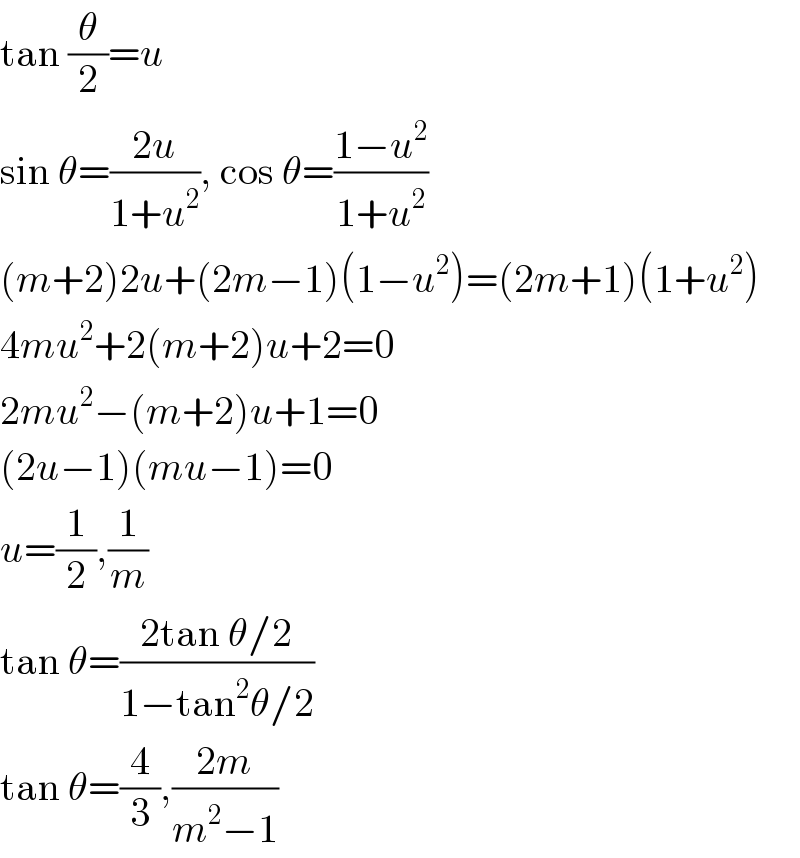
$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={u} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} },\:\mathrm{cos}\:\theta=\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\left({m}+\mathrm{2}\right)\mathrm{2}{u}+\left(\mathrm{2}{m}−\mathrm{1}\right)\left(\mathrm{1}−{u}^{\mathrm{2}} \right)=\left(\mathrm{2}{m}+\mathrm{1}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{mu}^{\mathrm{2}} +\mathrm{2}\left({m}+\mathrm{2}\right){u}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2}{mu}^{\mathrm{2}} −\left({m}+\mathrm{2}\right){u}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}{u}−\mathrm{1}\right)\left({mu}−\mathrm{1}\right)=\mathrm{0} \\ $$$${u}=\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{{m}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2tan}\:\theta/\mathrm{2}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \theta/\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{2}{m}}{{m}^{\mathrm{2}} −\mathrm{1}} \\ $$
Commented by Tinkutara last updated on 17/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by ajfour last updated on 16/Jul/17
![(√((m+2)^2 +(2m−1)^2 ))sin (θ+tan^(−1) ((2m−1)/(m+2)))=2m+1 θ=−tan^(−1) ((2m−1)/(m+2))+sin^(−1) ((2m+1)/(√((m−2)^2 +(2m+1)^2 ))) =−tan^(−1) ((2m−1)/(m+2))+tan^(−1) ((2m+1)/(m−2)) tan θ=((((2m+1)/(m−2))−((2m−1)/(m+2)))/(1+((2m+1)/(m−2)).((2m−1)/(m+2)))) = (((2m+1)(m+2)−(2m−1)(m−2))/(m^2 −4+4m^2 −1)) tan θ=((10m)/(5(m^2 −1))) =((2m)/(m^2 −1)) . [ option (3) ,(2) ] for m=2 , tan θ=(4/3).](Q18189.png)
$$\sqrt{\left(\mathrm{m}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{2m}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{sin}\:\left(\theta+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2m}−\mathrm{1}}{\mathrm{m}+\mathrm{2}}\right)=\mathrm{2m}+\mathrm{1} \\ $$$$\theta=−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2m}−\mathrm{1}}{\mathrm{m}+\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2m}+\mathrm{1}}{\sqrt{\left(\mathrm{m}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{2m}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\:\:=−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2m}−\mathrm{1}}{\mathrm{m}+\mathrm{2}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2m}+\mathrm{1}}{\mathrm{m}−\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta=\frac{\frac{\mathrm{2m}+\mathrm{1}}{\mathrm{m}−\mathrm{2}}−\frac{\mathrm{2m}−\mathrm{1}}{\mathrm{m}+\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{2m}+\mathrm{1}}{\mathrm{m}−\mathrm{2}}.\frac{\mathrm{2m}−\mathrm{1}}{\mathrm{m}+\mathrm{2}}} \\ $$$$\:\:=\:\frac{\left(\mathrm{2m}+\mathrm{1}\right)\left(\mathrm{m}+\mathrm{2}\right)−\left(\mathrm{2m}−\mathrm{1}\right)\left(\mathrm{m}−\mathrm{2}\right)}{\mathrm{m}^{\mathrm{2}} −\mathrm{4}+\mathrm{4m}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\mathrm{tan}\:\theta=\frac{\mathrm{10m}}{\mathrm{5}\left(\mathrm{m}^{\mathrm{2}} −\mathrm{1}\right)}\:=\frac{\mathrm{2m}}{\mathrm{m}^{\mathrm{2}} −\mathrm{1}}\:. \\ $$$$\:\:\:\:\left[\:\mathrm{option}\:\:\left(\mathrm{3}\right)\:,\left(\mathrm{2}\right)\:\right] \\ $$$$\:\:\:\mathrm{for}\:\:\mathrm{m}=\mathrm{2}\:,\:\:\:\mathrm{tan}\:\theta=\frac{\mathrm{4}}{\mathrm{3}}. \\ $$
Commented by ajfour last updated on 16/Jul/17

$$\mathrm{you}\:\mathrm{can}\:\mathrm{view}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{Q}.\mathrm{18111} \\ $$$$\left(\mathrm{chord}\:\mathrm{AB}\:\mathrm{at}\:\angle=\phi\:\mathrm{with}\:\mathrm{diameter}\right. \\ $$$$\left.\mathrm{cut}\:\mathrm{in}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{p}:\mathrm{q}\:\right) \\ $$
Commented by Tinkutara last updated on 16/Jul/17

$$\mathrm{I}\:\mathrm{viewed}\:\mathrm{it}.\:\mathrm{Nice}\:\mathrm{method}!\:\mathrm{And}\:\mathrm{thanks} \\ $$$$\mathrm{for}\:\mathrm{this}\:\mathrm{solution}! \\ $$
