
Question Number 181779 by DAVONG last updated on 30/Nov/22
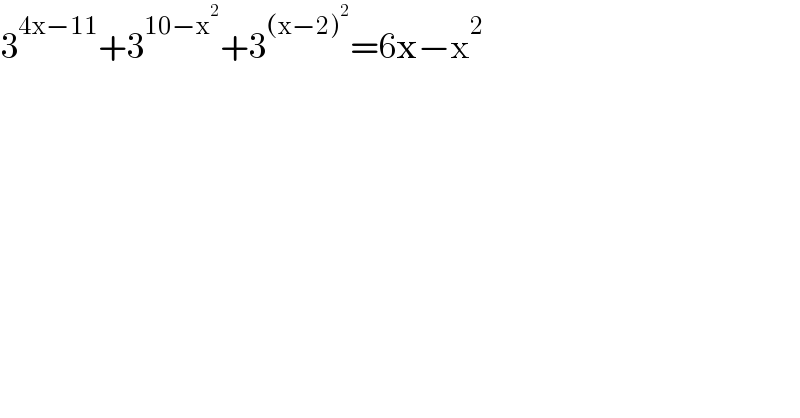
$$\mathrm{3}^{\mathrm{4x}−\mathrm{11}} +\mathrm{3}^{\mathrm{10}−\mathrm{x}^{\mathrm{2}} } +\mathrm{3}^{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} } =\mathrm{6x}−\mathrm{x}^{\mathrm{2}} \\ $$
Answered by manxsol last updated on 01/Dec/22
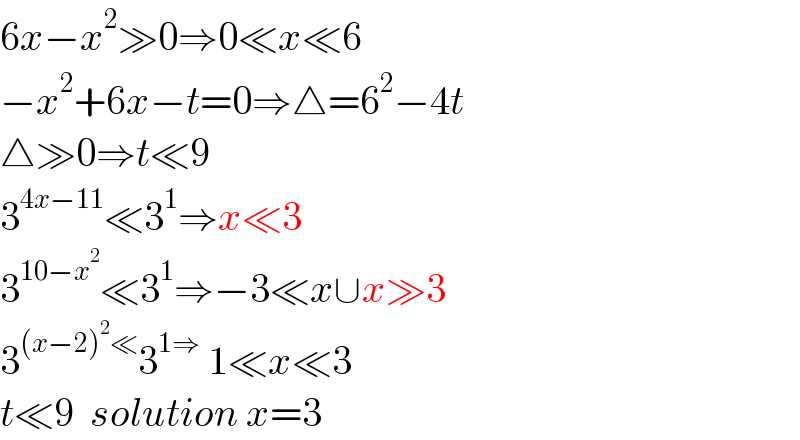
$$\mathrm{6}{x}−{x}^{\mathrm{2}} \gg\mathrm{0}\Rightarrow\mathrm{0}\ll{x}\ll\mathrm{6} \\ $$$$−{x}^{\mathrm{2}} +\mathrm{6}{x}−{t}=\mathrm{0}\Rightarrow\bigtriangleup=\mathrm{6}^{\mathrm{2}} −\mathrm{4}{t} \\ $$$$\bigtriangleup\gg\mathrm{0}\Rightarrow{t}\ll\mathrm{9} \\ $$$$\mathrm{3}^{\mathrm{4}{x}−\mathrm{11}} \ll\mathrm{3}^{\mathrm{1}} \Rightarrow{x}\ll\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{10}−{x}^{\mathrm{2}} } \ll\mathrm{3}^{\mathrm{1}} \Rightarrow−\mathrm{3}\ll{x}\cup{x}\gg\mathrm{3} \\ $$$$\mathrm{3}^{\left({x}−\mathrm{2}\right)^{\mathrm{2}} \ll} \mathrm{3}^{\mathrm{1}\Rightarrow} \:\mathrm{1}\ll{x}\ll\mathrm{3} \\ $$$${t}\ll\mathrm{9}\:\:{solution}\:{x}=\mathrm{3} \\ $$
