
Question Number 181764 by Mastermind last updated on 30/Nov/22
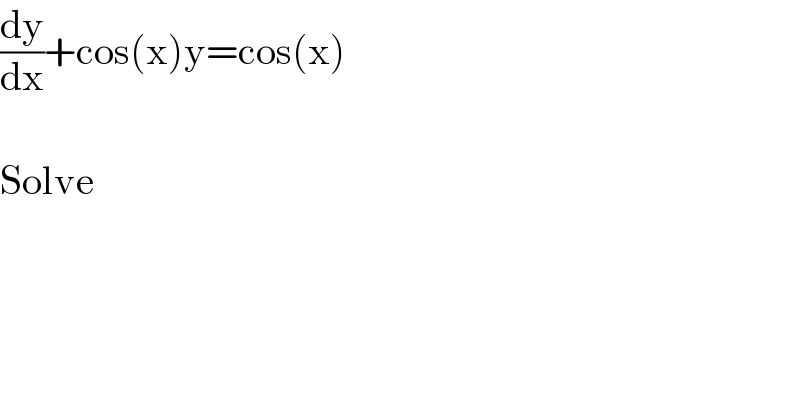
$$\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{cos}\left(\mathrm{x}\right)\mathrm{y}=\mathrm{cos}\left(\mathrm{x}\right) \\ $$$$ \\ $$$$\mathrm{Solve} \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 30/Nov/22
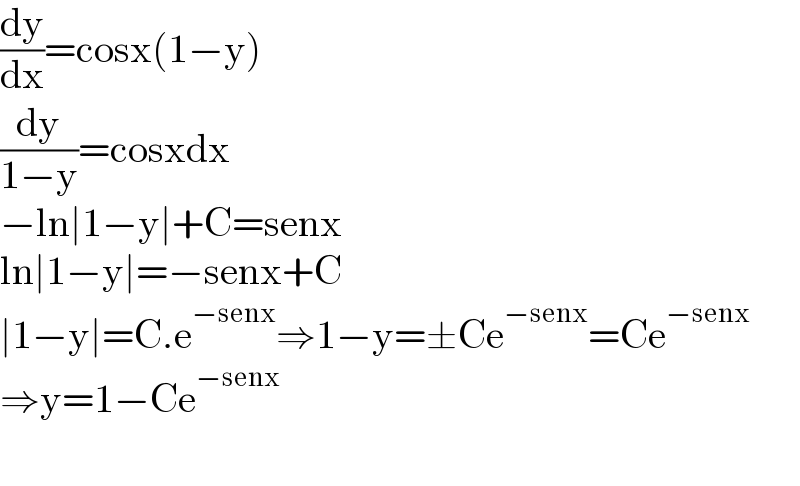
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{cosx}\left(\mathrm{1}−\mathrm{y}\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{1}−\mathrm{y}}=\mathrm{cosxdx} \\ $$$$−\mathrm{ln}\mid\mathrm{1}−\mathrm{y}\mid+\mathrm{C}=\mathrm{senx} \\ $$$$\mathrm{ln}\mid\mathrm{1}−\mathrm{y}\mid=−\mathrm{senx}+\mathrm{C} \\ $$$$\mid\mathrm{1}−\mathrm{y}\mid=\mathrm{C}.\mathrm{e}^{−\mathrm{senx}} \Rightarrow\mathrm{1}−\mathrm{y}=\pm\mathrm{Ce}^{−\mathrm{senx}} =\mathrm{Ce}^{−\mathrm{senx}} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{1}−\mathrm{Ce}^{−\mathrm{senx}} \\ $$$$ \\ $$
Answered by CElcedricjunior last updated on 30/Nov/22

$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\boldsymbol{{cosxy}}=\boldsymbol{{cosx}} \\ $$$$\boldsymbol{{or}}\:\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\boldsymbol{{y}}'=>\boldsymbol{{y}}'+\left(\boldsymbol{{cosx}}\right)\boldsymbol{{y}}=\boldsymbol{{cosx}} \\ $$$$\boldsymbol{{eqt}}\:\boldsymbol{{homogene}} \\ $$$$\boldsymbol{{y}}'+\left(\boldsymbol{{cosx}}\right)\boldsymbol{{y}}=\mathrm{0}=>\boldsymbol{{y}}_{\mathrm{0}} =\boldsymbol{{e}}^{\int−\boldsymbol{{cosxdx}}} \\ $$$$\boldsymbol{{y}}_{\mathrm{0}} =\boldsymbol{{ke}}^{−\boldsymbol{{sinx}}} \\ $$$$\boldsymbol{{faisons}}\:\boldsymbol{{varier}}\:\boldsymbol{{k}} \\ $$$$\boldsymbol{{y}}=\boldsymbol{{k}}\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} \\ $$$$\boldsymbol{{y}}'=\boldsymbol{{k}}'\left({x}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} −\boldsymbol{{cosxk}}\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} \\ $$$$\boldsymbol{{y}}'+\boldsymbol{{cosx}}\:\boldsymbol{{y}}=\boldsymbol{{cosx}} \\ $$$$=>\boldsymbol{{k}}'\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} −\boldsymbol{{cosxk}}\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} +\boldsymbol{{c}}{os}\boldsymbol{{xk}}\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} =\boldsymbol{{cosx}} \\ $$$$=>\boldsymbol{{k}}'\left({x}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} =\boldsymbol{{cosx}} \\ $$$$=>\boldsymbol{{k}}'\left(\boldsymbol{{x}}\right)=\boldsymbol{{cosx}}\:\boldsymbol{{e}}^{\boldsymbol{{sinx}}} \\ $$$$\boldsymbol{{k}}\left(\boldsymbol{{x}}\right)=\int\boldsymbol{{cosxe}}^{\boldsymbol{{sinx}}} \boldsymbol{{dx}}=\boldsymbol{{e}}^{\boldsymbol{{sinx}}} +\boldsymbol{{c}}\:\:{c}\in\mathbb{R} \\ $$$$\boldsymbol{{donc}} \\ $$$$\boldsymbol{{y}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{k}}\left(\boldsymbol{{x}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} =\left(\boldsymbol{{e}}^{\boldsymbol{{sinx}}} +\boldsymbol{{c}}\right)\boldsymbol{{e}}^{−\boldsymbol{{sinx}}} \\ $$$$\boldsymbol{{y}}\left(\boldsymbol{{x}}\right)=\mathrm{1}+\boldsymbol{{ce}}^{−\boldsymbol{{sinx}}} \\ $$$$........\overset{======================} {.} \\ $$$$===================== \\ $$
Answered by ali009 last updated on 30/Nov/22
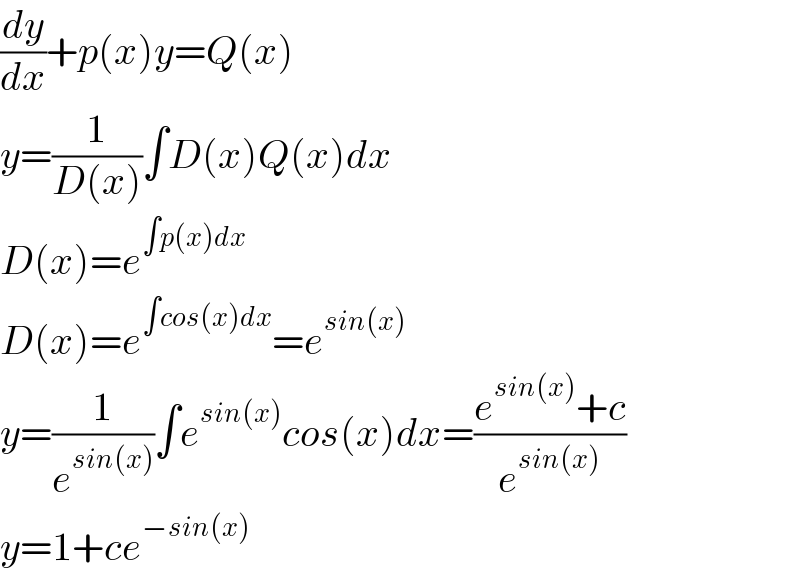
$$\frac{{dy}}{{dx}}+{p}\left({x}\right){y}={Q}\left({x}\right) \\ $$$${y}=\frac{\mathrm{1}}{{D}\left({x}\right)}\int{D}\left({x}\right){Q}\left({x}\right){dx} \\ $$$${D}\left({x}\right)={e}^{\int{p}\left({x}\right){dx}} \\ $$$${D}\left({x}\right)={e}^{\int{cos}\left({x}\right){dx}} ={e}^{{sin}\left({x}\right)} \\ $$$${y}=\frac{\mathrm{1}}{{e}^{{sin}\left({x}\right)} }\int{e}^{{sin}\left({x}\right)} {cos}\left({x}\right){dx}=\frac{{e}^{{sin}\left({x}\right)} +{c}}{{e}^{{sin}\left({x}\right)} } \\ $$$${y}=\mathrm{1}+{ce}^{−{sin}\left({x}\right)} \\ $$
