
Question Number 181747 by SANOGO last updated on 29/Nov/22
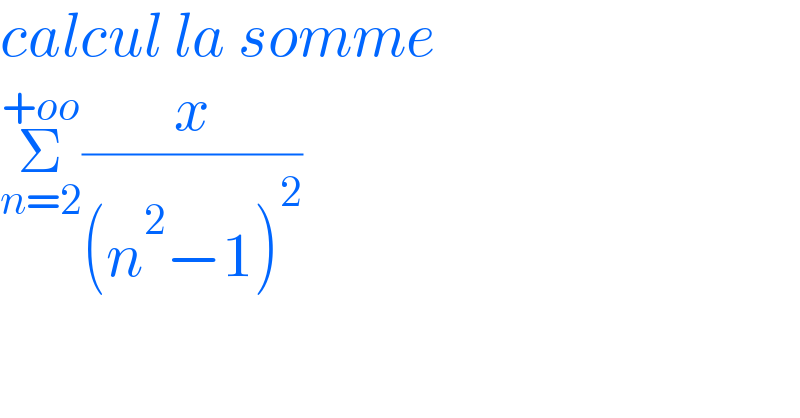
$${calcul}\:{la}\:{somme} \\ $$$$\underset{{n}=\mathrm{2}} {\overset{+{oo}} {\sum}}\frac{{x}}{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by Frix last updated on 01/Dec/22
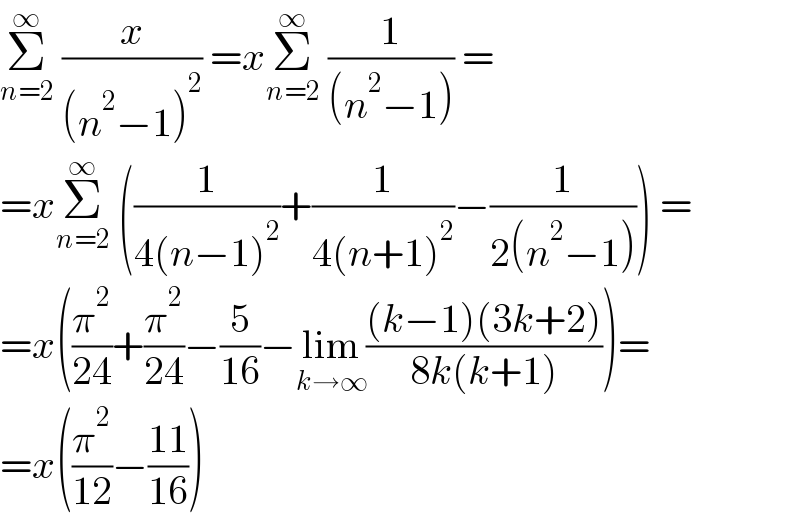
$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{{x}}{\left({n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:={x}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} −\mathrm{1}\right)}\:= \\ $$$$={x}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{4}\left({n}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}\left({n}^{\mathrm{2}} −\mathrm{1}\right)}\right)\:= \\ $$$$={x}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{\pi^{\mathrm{2}} }{\mathrm{24}}−\frac{\mathrm{5}}{\mathrm{16}}−\underset{{k}\rightarrow\infty} {\mathrm{lim}}\frac{\left({k}−\mathrm{1}\right)\left(\mathrm{3}{k}+\mathrm{2}\right)}{\mathrm{8}{k}\left({k}+\mathrm{1}\right)}\right)= \\ $$$$={x}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{11}}{\mathrm{16}}\right) \\ $$
