
Question Number 1817 by 112358 last updated on 05/Oct/15
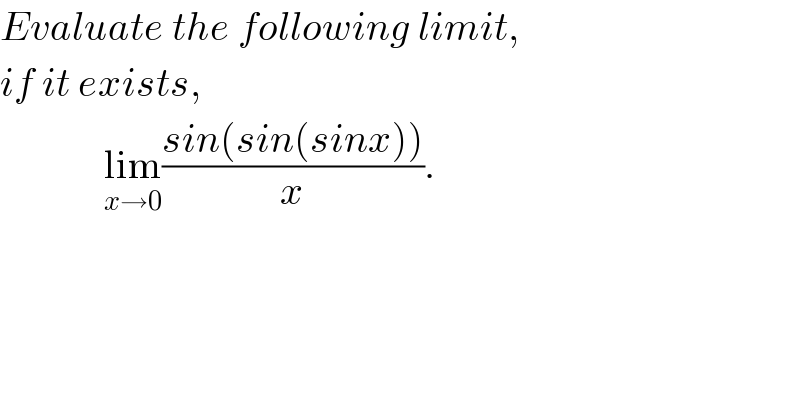
$${Evaluate}\:{the}\:{following}\:{limit}, \\ $$$${if}\:{it}\:{exists}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left({sin}\left({sinx}\right)\right)}{{x}}. \\ $$
Answered by 123456 last updated on 05/Oct/15
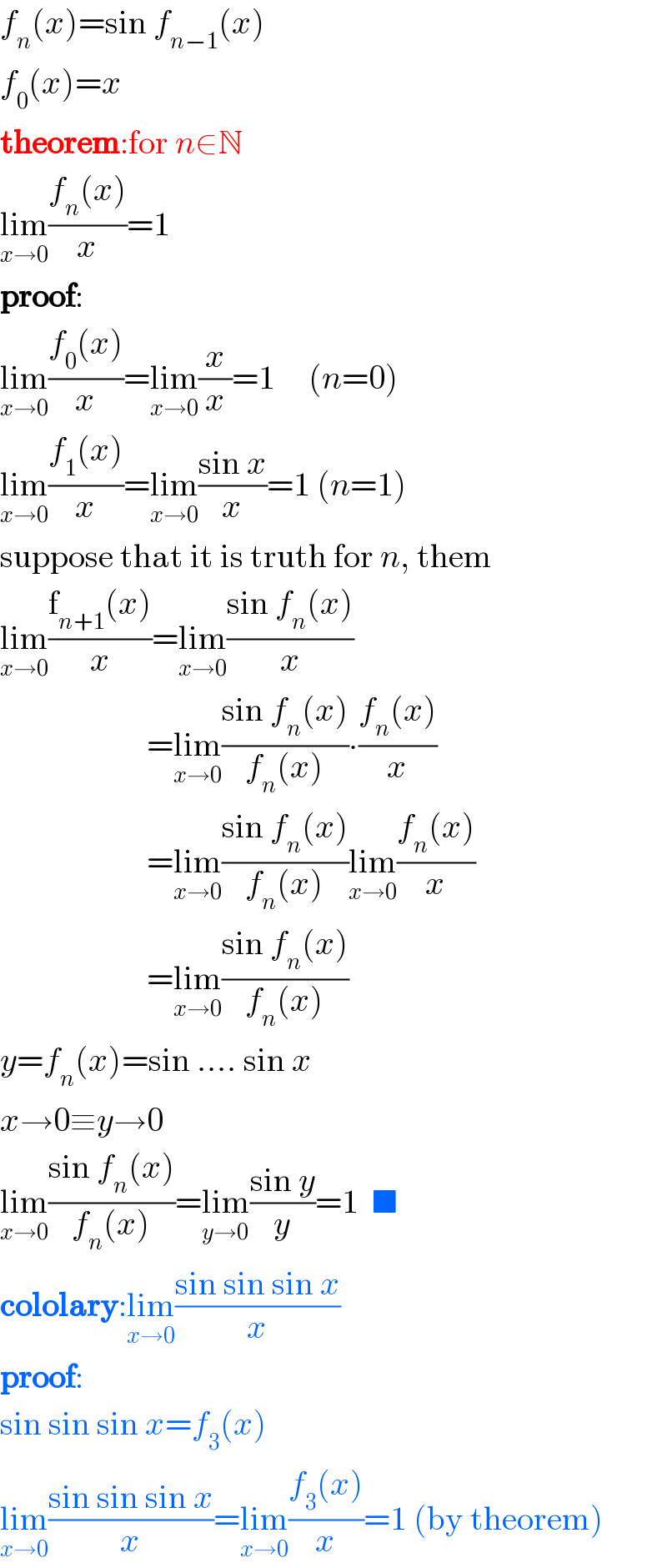
$${f}_{{n}} \left({x}\right)=\mathrm{sin}\:{f}_{{n}−\mathrm{1}} \left({x}\right) \\ $$$${f}_{\mathrm{0}} \left({x}\right)={x} \\ $$$$\boldsymbol{\mathrm{theorem}}:\mathrm{for}\:{n}\in\mathbb{N} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}_{{n}} \left({x}\right)}{{x}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{proof}}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}_{\mathrm{0}} \left({x}\right)}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{{x}}=\mathrm{1}\:\:\:\:\:\left({n}=\mathrm{0}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}_{\mathrm{1}} \left({x}\right)}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{{x}}=\mathrm{1}\:\left({n}=\mathrm{1}\right) \\ $$$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{truth}\:\mathrm{for}\:{n},\:\mathrm{them} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{f}_{{n}+\mathrm{1}} \left({x}\right)}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{f}_{{n}} \left({x}\right)}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{f}_{{n}} \left({x}\right)}{{f}_{{n}} \left({x}\right)}\centerdot\frac{{f}_{{n}} \left({x}\right)}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{f}_{{n}} \left({x}\right)}{{f}_{{n}} \left({x}\right)}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}_{{n}} \left({x}\right)}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{f}_{{n}} \left({x}\right)}{{f}_{{n}} \left({x}\right)} \\ $$$${y}={f}_{{n}} \left({x}\right)=\mathrm{sin}\:....\:\mathrm{sin}\:{x} \\ $$$${x}\rightarrow\mathrm{0}\equiv{y}\rightarrow\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{f}_{{n}} \left({x}\right)}{{f}_{{n}} \left({x}\right)}=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{y}}{{y}}=\mathrm{1}\:\:\blacksquare \\ $$$$\boldsymbol{\mathrm{cololary}}:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{sin}\:\mathrm{sin}\:{x}}{{x}} \\ $$$$\boldsymbol{\mathrm{proof}}: \\ $$$$\mathrm{sin}\:\mathrm{sin}\:\mathrm{sin}\:{x}={f}_{\mathrm{3}} \left({x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{sin}\:\mathrm{sin}\:{x}}{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}_{\mathrm{3}} \left({x}\right)}{{x}}=\mathrm{1}\:\left(\mathrm{by}\:\mathrm{theorem}\right) \\ $$
