
Question Number 18168 by allizzwell last updated on 16/Jul/17

$$\mathrm{If}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{the}\:\mathrm{middle}\:\mathrm{term}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\mathrm{the}\:\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}+\mathrm{2}} \:\mathrm{is}\:{p}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{middle}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}+\mathrm{1}} \:\mathrm{are}\:{q}\:\mathrm{and}\:{r},\:\mathrm{then} \\ $$
Answered by ajfour last updated on 16/Jul/17
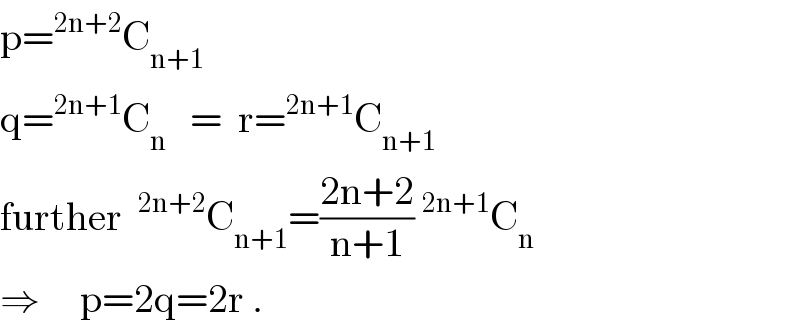
$$\mathrm{p}=^{\mathrm{2n}+\mathrm{2}} \mathrm{C}_{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{q}=^{\mathrm{2n}+\mathrm{1}} \mathrm{C}_{\mathrm{n}} \:\:\:=\:\:\mathrm{r}=^{\mathrm{2n}+\mathrm{1}} \mathrm{C}_{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{further}\:\:^{\mathrm{2n}+\mathrm{2}} \mathrm{C}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{2n}+\mathrm{2}}{\mathrm{n}+\mathrm{1}}\:^{\mathrm{2n}+\mathrm{1}} \mathrm{C}_{\mathrm{n}} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{p}=\mathrm{2q}=\mathrm{2r}\:. \\ $$
