
Question Number 181599 by CrispyXYZ last updated on 27/Nov/22
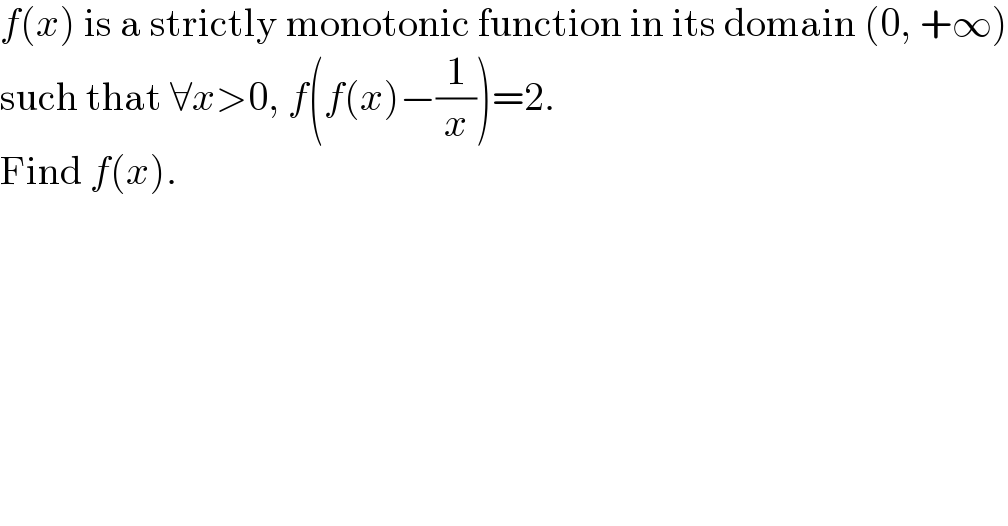
$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{strictly}\:\mathrm{monotonic}\:\mathrm{function}\:\mathrm{in}\:\mathrm{its}\:\mathrm{domain}\:\left(\mathrm{0},\:+\infty\right) \\ $$ $$\mathrm{such}\:\mathrm{that}\:\forall{x}>\mathrm{0},\:{f}\left({f}\left({x}\right)−\frac{\mathrm{1}}{{x}}\right)=\mathrm{2}. \\ $$ $$\mathrm{Find}\:{f}\left({x}\right). \\ $$
Answered by mr W last updated on 27/Nov/22
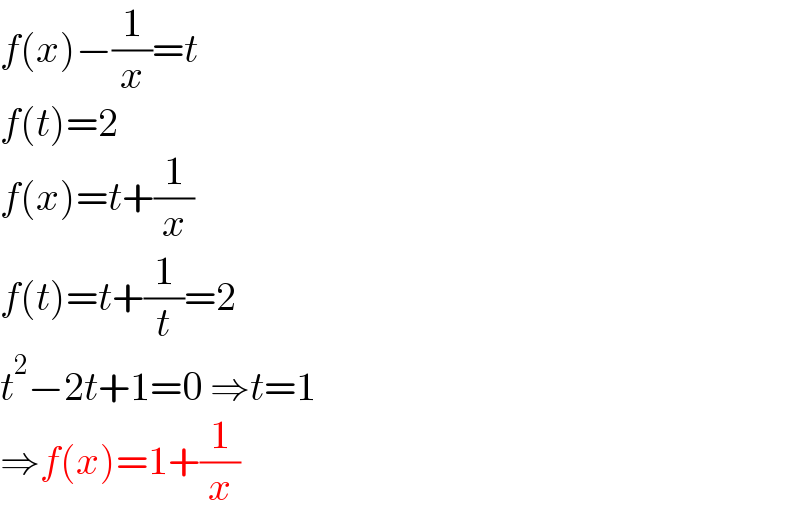
$${f}\left({x}\right)−\frac{\mathrm{1}}{{x}}={t} \\ $$ $${f}\left({t}\right)=\mathrm{2} \\ $$ $${f}\left({x}\right)={t}+\frac{\mathrm{1}}{{x}} \\ $$ $${f}\left({t}\right)={t}+\frac{\mathrm{1}}{{t}}=\mathrm{2}\: \\ $$ $${t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}=\mathrm{0}\:\Rightarrow{t}=\mathrm{1} \\ $$ $$\Rightarrow{f}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{{x}} \\ $$
