
Question Number 181509 by Mastermind last updated on 26/Nov/22
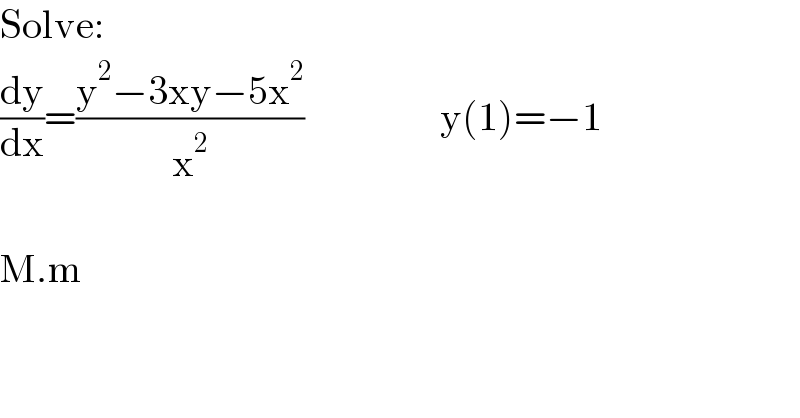
$$\mathrm{Solve}: \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{y}^{\mathrm{2}} −\mathrm{3xy}−\mathrm{5x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\left(\mathrm{1}\right)=−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by BaliramKumar last updated on 26/Nov/22
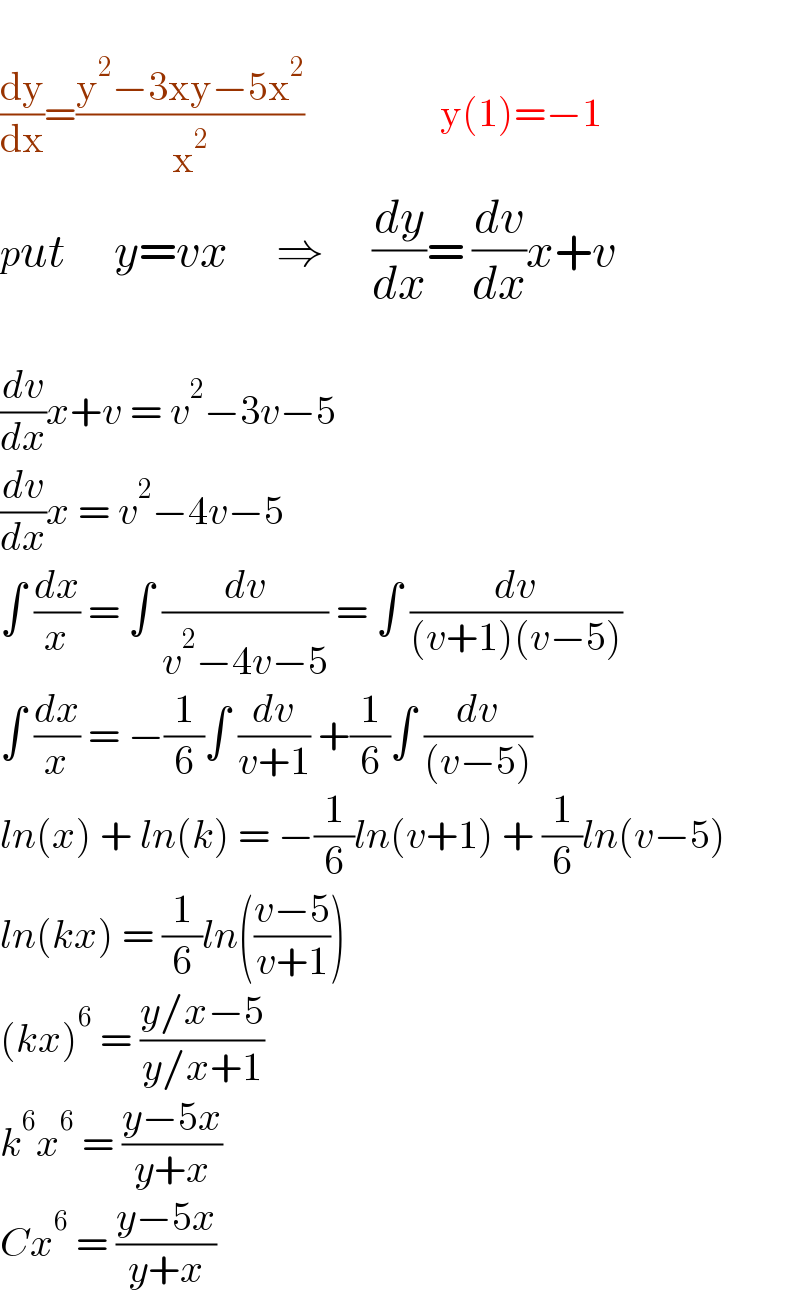
$$ \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{y}^{\mathrm{2}} −\mathrm{3xy}−\mathrm{5x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\left(\mathrm{1}\right)=−\mathrm{1} \\ $$$${put}\:\:\:\:\:\:{y}={vx}\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\frac{{dy}}{{dx}}=\:\frac{{dv}}{{dx}}{x}+{v} \\ $$$$ \\ $$$$\frac{{dv}}{{dx}}{x}+{v}\:=\:{v}^{\mathrm{2}} −\mathrm{3}{v}−\mathrm{5} \\ $$$$\frac{{dv}}{{dx}}{x}\:=\:{v}^{\mathrm{2}} −\mathrm{4}{v}−\mathrm{5} \\ $$$$\int\:\frac{{dx}}{{x}}\:=\:\int\:\frac{{dv}}{{v}^{\mathrm{2}} −\mathrm{4}{v}−\mathrm{5}}\:=\:\int\:\frac{{dv}}{\left({v}+\mathrm{1}\right)\left({v}−\mathrm{5}\right)} \\ $$$$\int\:\frac{{dx}}{{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\int\:\frac{{dv}}{{v}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{6}}\int\:\frac{{dv}}{\left({v}−\mathrm{5}\right)} \\ $$$${ln}\left({x}\right)\:+\:{ln}\left({k}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({v}+\mathrm{1}\right)\:+\:\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({v}−\mathrm{5}\right) \\ $$$${ln}\left({kx}\right)\:=\:\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\frac{{v}−\mathrm{5}}{{v}+\mathrm{1}}\right) \\ $$$$\left({kx}\right)^{\mathrm{6}} \:=\:\frac{{y}/{x}−\mathrm{5}}{{y}/{x}+\mathrm{1}} \\ $$$${k}^{\mathrm{6}} {x}^{\mathrm{6}} \:=\:\frac{{y}−\mathrm{5}{x}}{{y}+{x}} \\ $$$${Cx}^{\mathrm{6}} \:=\:\frac{{y}−\mathrm{5}{x}}{{y}+{x}} \\ $$
