
Question Number 180828 by Vynho last updated on 17/Nov/22
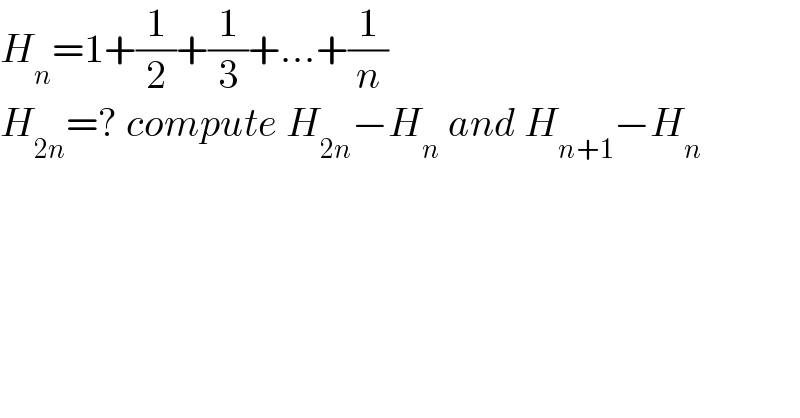
$${H}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}} \\ $$$${H}_{\mathrm{2}{n}} =?\:{compute}\:{H}_{\mathrm{2}{n}} −{H}_{{n}} \:{and}\:{H}_{{n}+\mathrm{1}} −{H}_{{n}} \\ $$
Commented by Frix last updated on 17/Nov/22
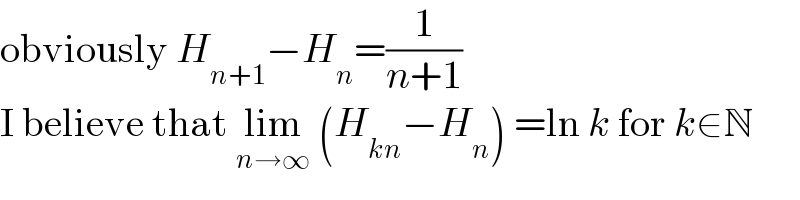
$$\mathrm{obviously}\:{H}_{{n}+\mathrm{1}} −{H}_{{n}} =\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}\:\mathrm{believe}\:\mathrm{that}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left({H}_{{kn}} −{H}_{{n}} \right)\:=\mathrm{ln}\:{k}\:\mathrm{for}\:{k}\in\mathbb{N} \\ $$
Answered by Frix last updated on 19/Nov/22
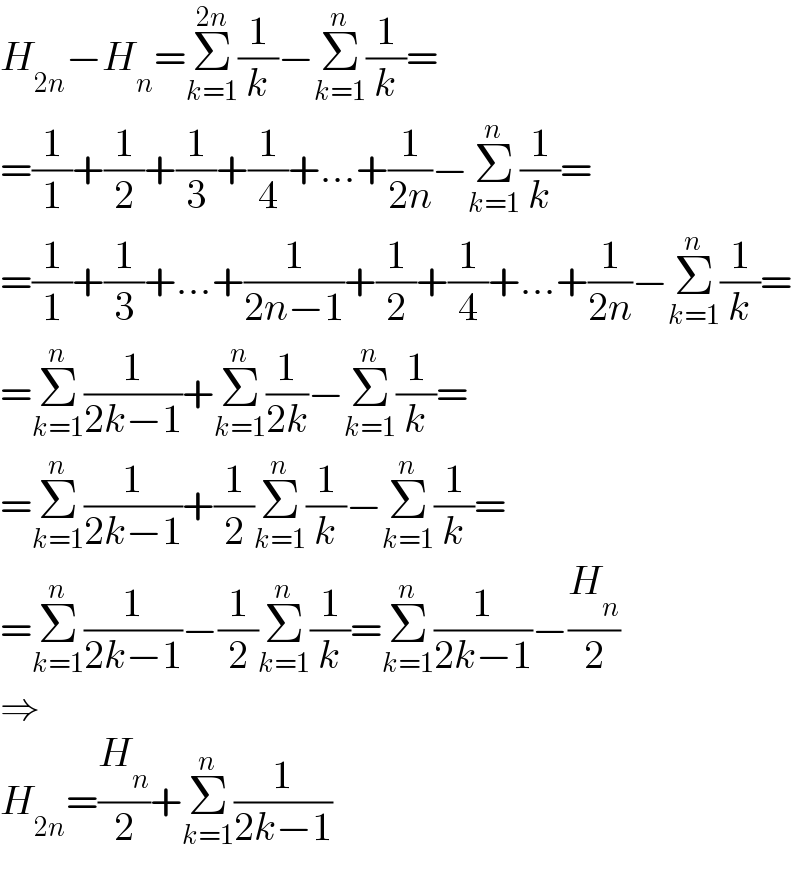
$${H}_{\mathrm{2}{n}} −{H}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\frac{\mathrm{1}}{{k}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{{H}_{{n}} }{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${H}_{\mathrm{2}{n}} =\frac{{H}_{{n}} }{\mathrm{2}}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}} \\ $$
