
Question Number 180446 by Mastermind last updated on 12/Nov/22
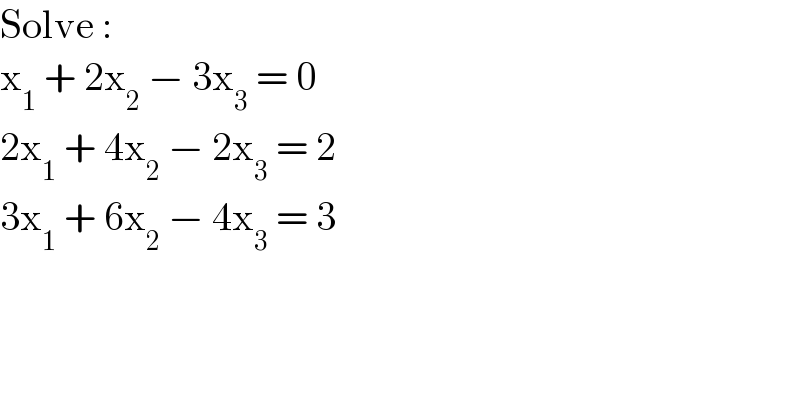
$$\mathrm{Solve}\::\: \\ $$$$\mathrm{x}_{\mathrm{1}} \:+\:\mathrm{2x}_{\mathrm{2}} \:−\:\mathrm{3x}_{\mathrm{3}} \:=\:\mathrm{0} \\ $$$$\mathrm{2x}_{\mathrm{1}} \:+\:\mathrm{4x}_{\mathrm{2}} \:−\:\mathrm{2x}_{\mathrm{3}} \:=\:\mathrm{2} \\ $$$$\mathrm{3x}_{\mathrm{1}} \:+\:\mathrm{6x}_{\mathrm{2}} \:−\:\mathrm{4x}_{\mathrm{3}} \:=\:\mathrm{3} \\ $$
Answered by liuxinnan last updated on 12/Nov/22

$$ \\ $$
Commented by liuxinnan last updated on 12/Nov/22
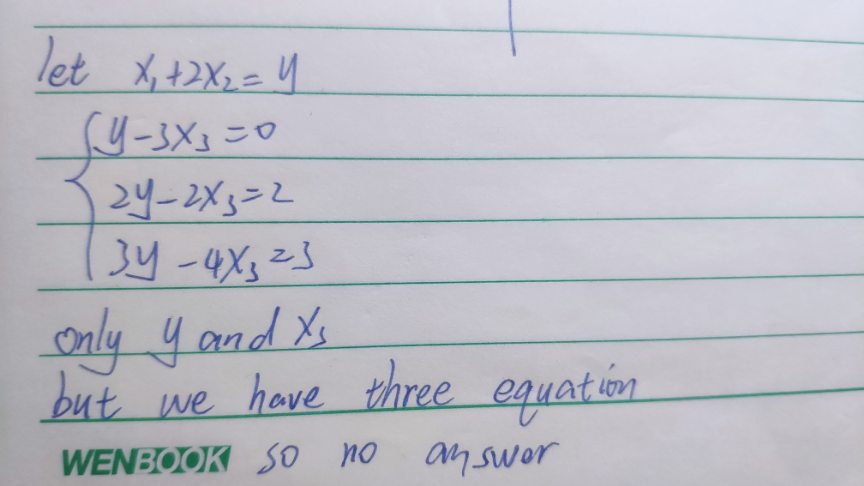
Answered by mr W last updated on 12/Nov/22

$${from}\:{eqn}.\:\left({i}\right)\:{we}\:{get}: \\ $$$$\mathrm{2}{x}_{\mathrm{1}} +\mathrm{4}{x}_{\mathrm{2}} =\mathrm{6}{x}_{\mathrm{3}} \:\:\:\:\:...\left({iv}\right) \\ $$$${from}\:\left({ii}\right)\:{and}\:\left({iv}\right): \\ $$$$\mathrm{6}{x}_{\mathrm{3}} =\mathrm{2}+\mathrm{2}{x}_{\mathrm{3}} \\ $$$$\Rightarrow{x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${from}\:{eqn}.\:\left({i}\right)\:{we}\:{get}: \\ $$$$\mathrm{3}{x}_{\mathrm{1}} +\mathrm{6}{x}_{\mathrm{2}} =\mathrm{9}{x}_{\mathrm{3}} \:\:\:\:\:...\left({v}\right) \\ $$$${from}\:\left({iii}\right)\:{and}\:\left({v}\right): \\ $$$$\mathrm{9}{x}_{\mathrm{3}} =\mathrm{3}+\mathrm{4}{x}_{\mathrm{3}} \\ $$$$\Rightarrow{x}_{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${this}\:{is}\:{contradiction}\:{to}\:{x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$${that}\:{means}\:{the}\:{eqn}.\:{system}\:{has}\:{no} \\ $$$${solution}. \\ $$
