
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 179906 by Acem last updated on 04/Nov/22

$$\mathrm{2}\:{boxes},\:\mathrm{1}{st}\:{contains}\:\mathrm{4}\:{white}\:\&\:\mathrm{6}\:{black}\:{balls} \\ $$ $$\:\mathrm{2}{nd}\:{box}\:{contains}\:\mathrm{8}\:{white}\:\&\:\mathrm{8}\:{black}\:{balls} \\ $$ $$\:{We}\:{randomly}\:{draw}\:{a}\:{ball},\:{got}\:{a}\:{black}\:{one} \\ $$ $$\:{What}'{s}\:{probability}\:{that}\:{it}\:{was}\:{drawn}\:{from}\:{Box}_{\mathrm{2}} ? \\ $$
Answered by som(math1967) last updated on 04/Nov/22
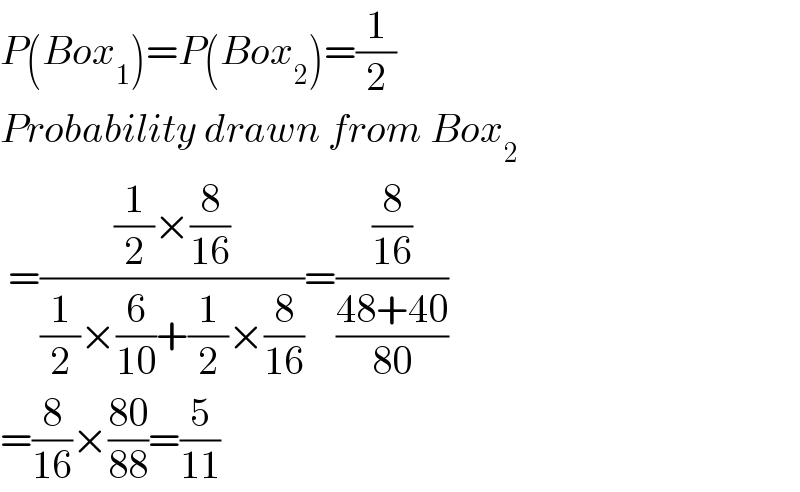
$${P}\left({Box}_{\mathrm{1}} \right)={P}\left({Box}_{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$ $${Probability}\:{drawn}\:{from}\:{Box}_{\mathrm{2}} \\ $$ $$\:=\frac{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{8}}{\mathrm{16}}}{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{6}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{8}}{\mathrm{16}}}=\frac{\frac{\mathrm{8}}{\mathrm{16}}}{\frac{\mathrm{48}+\mathrm{40}}{\mathrm{80}}} \\ $$ $$=\frac{\mathrm{8}}{\mathrm{16}}×\frac{\mathrm{80}}{\mathrm{88}}=\frac{\mathrm{5}}{\mathrm{11}}\: \\ $$
Commented byAcem last updated on 04/Nov/22
$${Correct}\:{answer},\:{thanks}! \\ $$
Answered by Acem last updated on 04/Nov/22
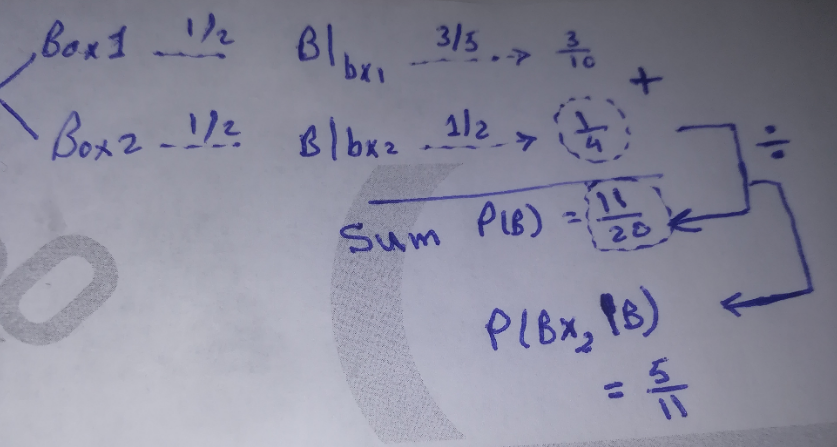
Commented byAcem last updated on 04/Nov/22
$${Summarize}\:{the}\:{solution}\:{by}\:{tree}\:{form} \\ $$
