Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 179886 by yaojunon2t last updated on 03/Nov/22

Commented by yaojunon2t last updated on 03/Nov/22

∵e^(iθ) =cos θ+i sin θ,θ=(π/2)+2kπ ∴e^(i((π/2)+2kπ)) =cos (π/2)+i sin (π/2) ∴e^(i((π/2)+2kπ)) =i ∴i^i =(e^(i((π/2)+2kπ)) )^i =e^(i^2 ((π/2)+2kπ)) =e^(−((π/2)+2kπ)) (k∈Z) ⇒i^i =e^((3π)/2) ,e^(−(π/2)) ,e^(−((5π)/2)) ,... ∴i^i ≈111.32,0.2079,0.000388...

$$\because{e}^{{i}\theta} =\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta,\theta=\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$$$\therefore{e}^{{i}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\right)} =\mathrm{cos}\:\frac{\pi}{\mathrm{2}}+{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}} \\ $$$$\therefore{e}^{{i}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\right)} ={i} \\ $$$$\therefore{i}^{{i}} =\left({e}^{{i}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\right)} \right)^{{i}} ={e}^{{i}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\right)} ={e}^{−\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\right)} \:\:\:\:\left({k}\in\mathbb{Z}\right) \\ $$$$\Rightarrow{i}^{{i}} ={e}^{\frac{\mathrm{3}\pi}{\mathrm{2}}} ,{e}^{−\frac{\pi}{\mathrm{2}}} ,{e}^{−\frac{\mathrm{5}\pi}{\mathrm{2}}} ,... \\ $$$$\therefore{i}^{{i}} \approx\mathrm{111}.\mathrm{32},\mathrm{0}.\mathrm{2079},\mathrm{0}.\mathrm{000388}... \\ $$

Commented by yaojunon2t last updated on 03/Nov/22

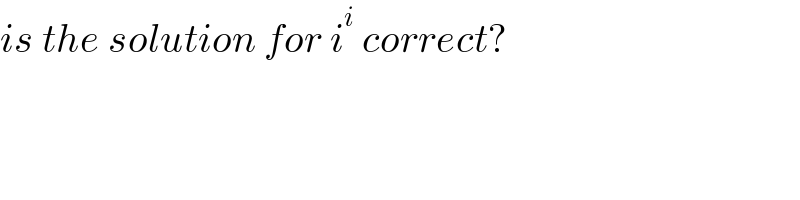
is the solution for i^i correct?

$${is}\:{the}\:{solution}\:{for}\:{i}^{{i}} \:{correct}? \\ $$

Commented by mr W last updated on 03/Nov/22

yes

$${yes} \\ $$

Commented by MJS_new last updated on 03/Nov/22

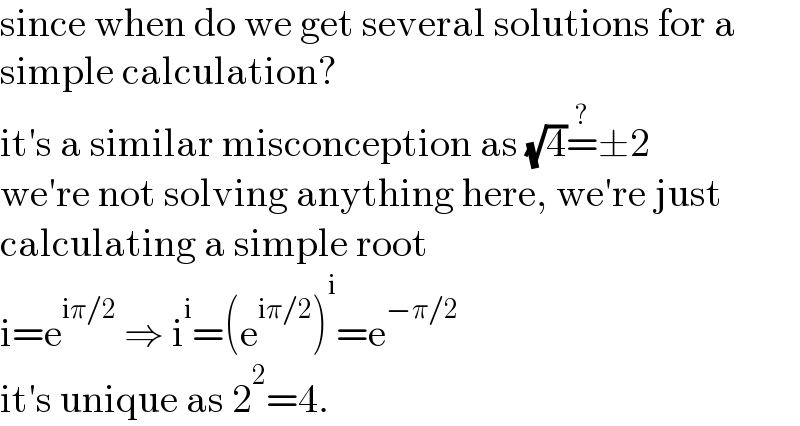
since when do we get several solutions for a simple calculation? it′s a similar misconception as (√4)=^? ±2 we′re not solving anything here, we′re just calculating a simple root i=e^(iπ/2) ⇒ i^i =(e^(iπ/2) )^i =e^(−π/2) it′s unique as 2^2 =4.

$$\mathrm{since}\:\mathrm{when}\:\mathrm{do}\:\mathrm{we}\:\mathrm{get}\:\mathrm{several}\:\mathrm{solutions}\:\mathrm{for}\:\mathrm{a} \\ $$$$\mathrm{simple}\:\mathrm{calculation}? \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{similar}\:\mathrm{misconception}\:\mathrm{as}\:\sqrt{\mathrm{4}}\overset{?} {=}\pm\mathrm{2} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{not}\:\mathrm{solving}\:\mathrm{anything}\:\mathrm{here},\:\mathrm{we}'\mathrm{re}\:\mathrm{just} \\ $$$$\mathrm{calculating}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{root} \\ $$$$\mathrm{i}=\mathrm{e}^{\mathrm{i}\pi/\mathrm{2}} \:\Rightarrow\:\mathrm{i}^{\mathrm{i}} =\left(\mathrm{e}^{\mathrm{i}\pi/\mathrm{2}} \right)^{\mathrm{i}} =\mathrm{e}^{−\pi/\mathrm{2}} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{unique}\:\mathrm{as}\:\mathrm{2}^{\mathrm{2}} =\mathrm{4}. \\ $$

Commented by yaojunon2t last updated on 04/Nov/22

thanks sir

$${thanks}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com