
Question Number 179453 by cherokeesay last updated on 29/Oct/22
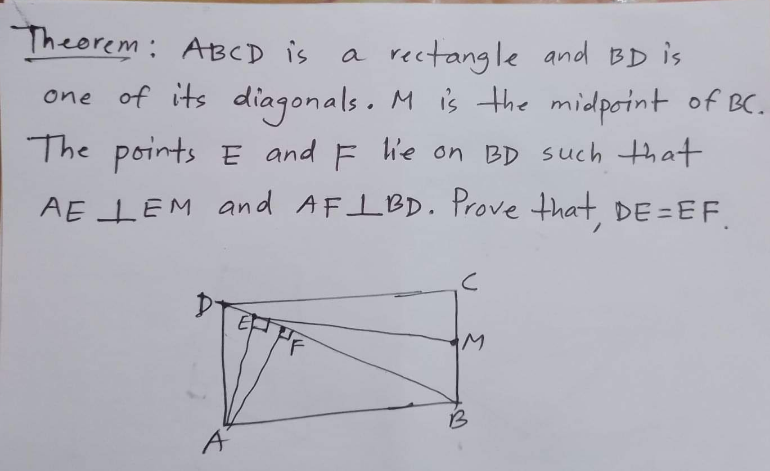
Answered by mr W last updated on 29/Oct/22
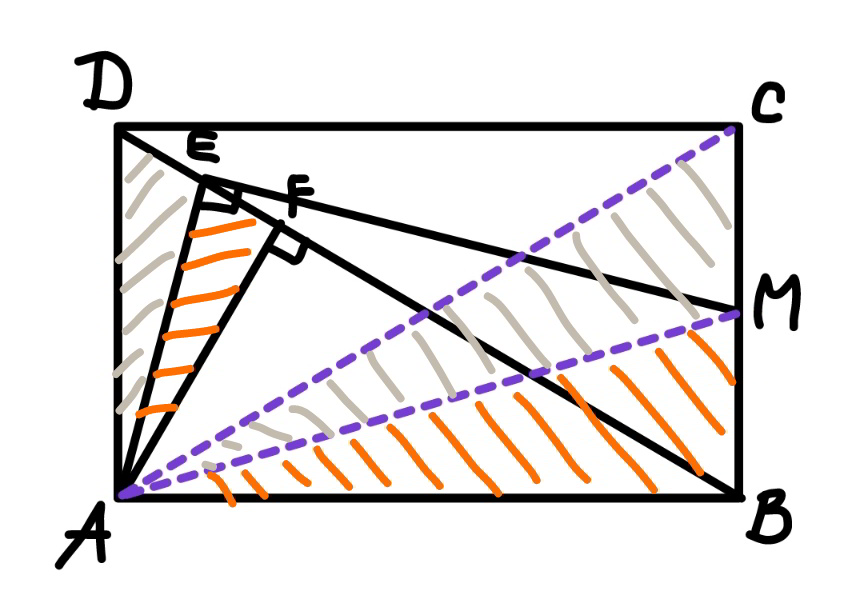
Commented by mr W last updated on 29/Oct/22
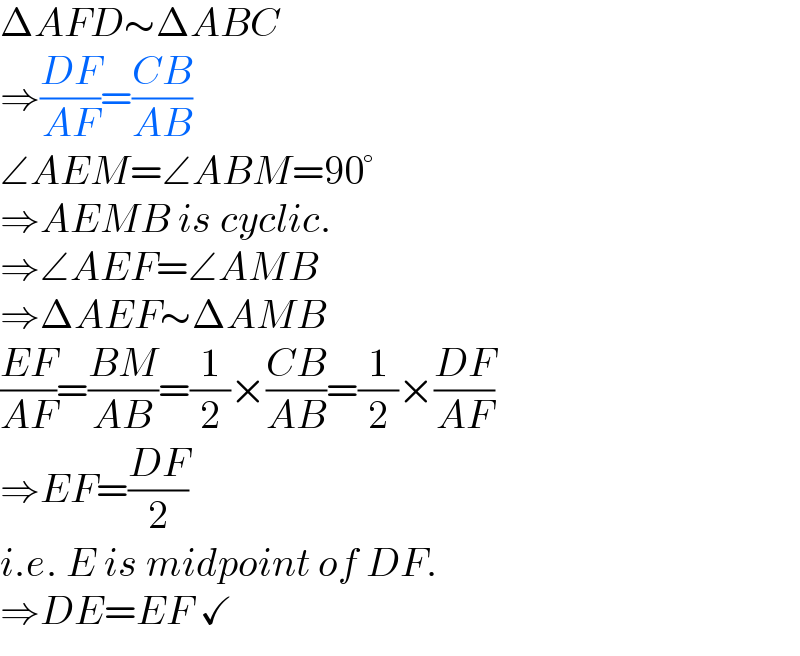
$$\Delta{AFD}\sim\Delta{ABC} \\ $$$$\Rightarrow\frac{{DF}}{{AF}}=\frac{{CB}}{{AB}} \\ $$$$\angle{AEM}=\angle{ABM}=\mathrm{90}° \\ $$$$\Rightarrow{AEMB}\:{is}\:{cyclic}. \\ $$$$\Rightarrow\angle{AEF}=\angle{AMB} \\ $$$$\Rightarrow\Delta{AEF}\sim\Delta{AMB} \\ $$$$\frac{{EF}}{{AF}}=\frac{{BM}}{{AB}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{CB}}{{AB}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{DF}}{{AF}} \\ $$$$\Rightarrow{EF}=\frac{{DF}}{\mathrm{2}} \\ $$$${i}.{e}.\:{E}\:{is}\:{midpoint}\:{of}\:{DF}. \\ $$$$\Rightarrow{DE}={EF}\:\checkmark \\ $$
Commented by cherokeesay last updated on 29/Oct/22

$${thank}\:{you}\:{so}\:{much}\:{master}. \\ $$
Commented by Tawa11 last updated on 30/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
