
Question Number 17921 by Tinkutara last updated on 12/Jul/17
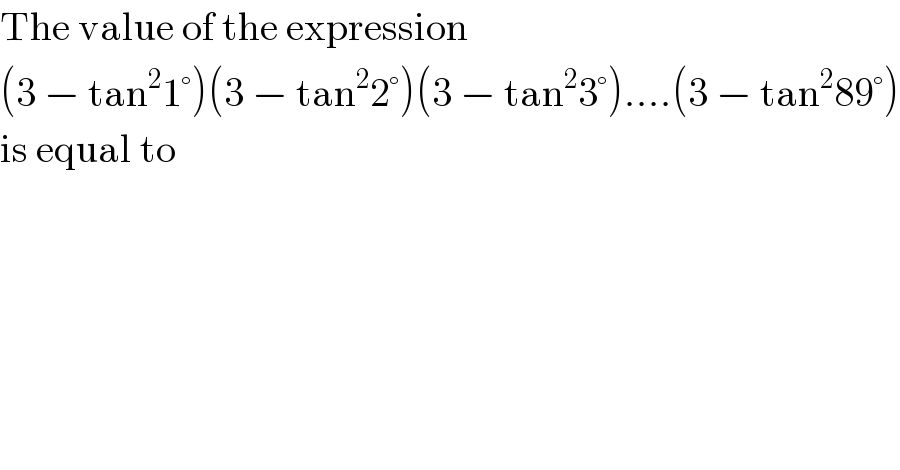
$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression} \\ $$$$\left(\mathrm{3}\:−\:\mathrm{tan}^{\mathrm{2}} \mathrm{1}°\right)\left(\mathrm{3}\:−\:\mathrm{tan}^{\mathrm{2}} \mathrm{2}°\right)\left(\mathrm{3}\:−\:\mathrm{tan}^{\mathrm{2}} \mathrm{3}°\right)....\left(\mathrm{3}\:−\:\mathrm{tan}^{\mathrm{2}} \mathrm{89}°\right) \\ $$$$\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$
Commented by Tinkutara last updated on 12/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{was}\:\mathrm{also}\:\mathrm{a} \\ $$$$\mathrm{term}! \\ $$
Commented by alex041103 last updated on 12/Jul/17
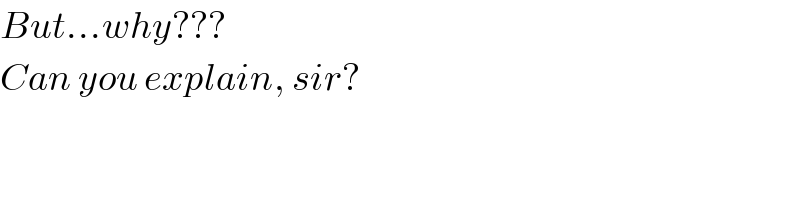
$${But}...{why}??? \\ $$$${Can}\:{you}\:{explain},\:{sir}? \\ $$
Commented by Tinkutara last updated on 12/Jul/17
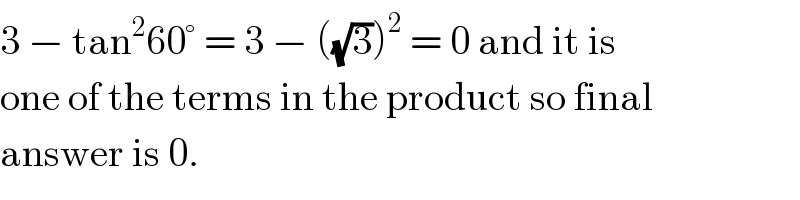
$$\mathrm{3}\:−\:\mathrm{tan}^{\mathrm{2}} \mathrm{60}°\:=\:\mathrm{3}\:−\:\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{product}\:\mathrm{so}\:\mathrm{final} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{0}. \\ $$
Commented by ajfour last updated on 12/Jul/17

$$\:\mathrm{3}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{60}°\:=\mathrm{0} \\ $$
Commented by alex041103 last updated on 12/Jul/17

$${thank}\:{you}\:{sir} \\ $$
