
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 178937 by Tawa11 last updated on 22/Oct/22

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{in}\:\mathrm{expansion}\:\mathrm{of}:\:\:\:\:\left(\mathrm{6}\:\:\:−\:\:\:\mathrm{4x}\right)^{−\:\:\mathrm{3}} \\ $$
Answered by mr W last updated on 23/Oct/22
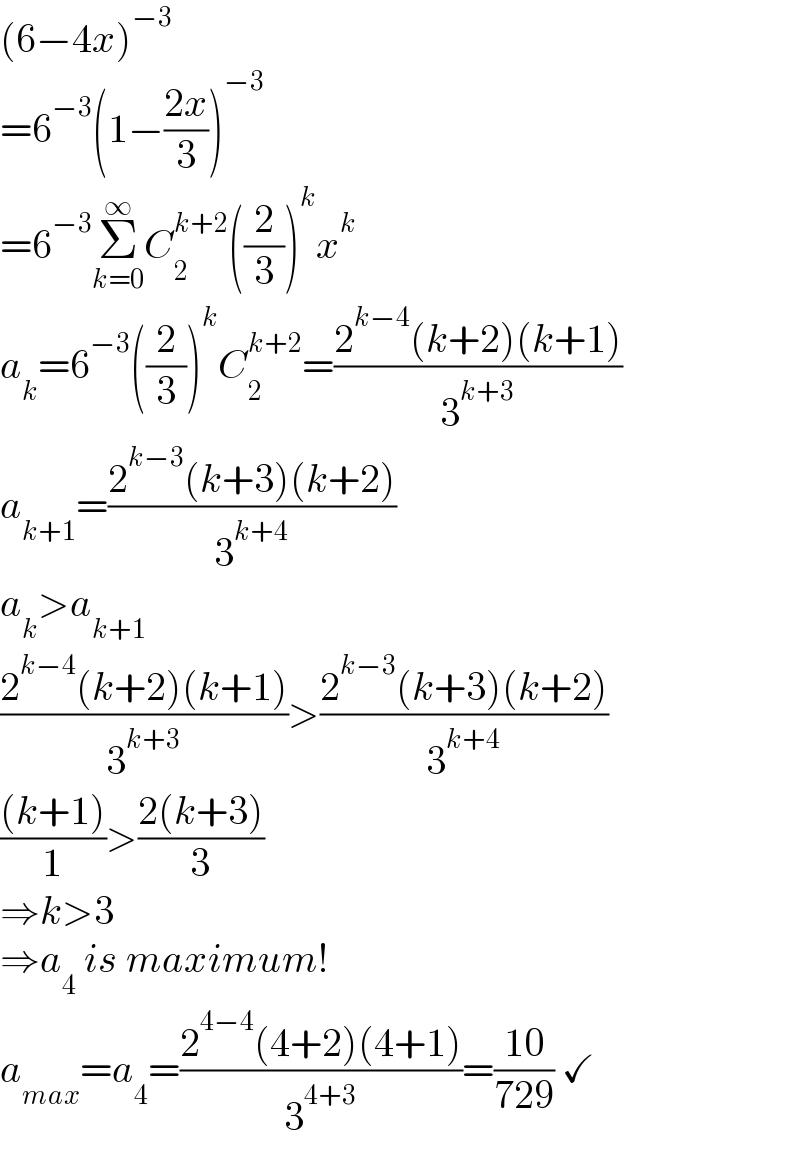
$$\left(\mathrm{6}−\mathrm{4}{x}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{6}^{−\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{3}}\right)^{−\mathrm{3}} \\ $$$$=\mathrm{6}^{−\mathrm{3}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{k}} {x}^{{k}} \\ $$$${a}_{{k}} =\mathrm{6}^{−\mathrm{3}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{k}} {C}_{\mathrm{2}} ^{{k}+\mathrm{2}} =\frac{\mathrm{2}^{{k}−\mathrm{4}} \left({k}+\mathrm{2}\right)\left({k}+\mathrm{1}\right)}{\mathrm{3}^{{k}+\mathrm{3}} } \\ $$$${a}_{{k}+\mathrm{1}} =\frac{\mathrm{2}^{{k}−\mathrm{3}} \left({k}+\mathrm{3}\right)\left({k}+\mathrm{2}\right)}{\mathrm{3}^{{k}+\mathrm{4}} } \\ $$$${a}_{{k}} >{a}_{{k}+\mathrm{1}} \\ $$$$\frac{\mathrm{2}^{{k}−\mathrm{4}} \left({k}+\mathrm{2}\right)\left({k}+\mathrm{1}\right)}{\mathrm{3}^{{k}+\mathrm{3}} }>\frac{\mathrm{2}^{{k}−\mathrm{3}} \left({k}+\mathrm{3}\right)\left({k}+\mathrm{2}\right)}{\mathrm{3}^{{k}+\mathrm{4}} } \\ $$$$\frac{\left({k}+\mathrm{1}\right)}{\mathrm{1}}>\frac{\mathrm{2}\left({k}+\mathrm{3}\right)}{\mathrm{3}} \\ $$$$\Rightarrow{k}>\mathrm{3} \\ $$$$\Rightarrow{a}_{\mathrm{4}} \:{is}\:{maximum}! \\ $$$${a}_{{max}} ={a}_{\mathrm{4}} =\frac{\mathrm{2}^{\mathrm{4}−\mathrm{4}} \left(\mathrm{4}+\mathrm{2}\right)\left(\mathrm{4}+\mathrm{1}\right)}{\mathrm{3}^{\mathrm{4}+\mathrm{3}} }=\frac{\mathrm{10}}{\mathrm{729}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 23/Oct/22
$$\mathrm{Great},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciare}. \\ $$
