
Question Number 178867 by Spillover last updated on 22/Oct/22

Answered by Spillover last updated on 15/Jan/23

$${f}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{7}{x}^{\mathrm{3}} +\mathrm{1} \\ $$$${requare}\:{to}\:{show} \\ $$$${f}\left({x}_{{o}} \right)×{f}\left({x}_{\mathrm{1}} \right)<\mathrm{0} \\ $$$${given}\:\:\mathrm{0}<{x}<\mathrm{1} \\ $$$${f}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{7}{x}^{\mathrm{3}} +\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1}\:\:\:{f}\left(\mathrm{1}\right)=−\mathrm{5} \\ $$$${f}\left({x}_{{o}} \right)×{f}\left({x}_{\mathrm{1}} \right)<\mathrm{0} \\ $$$$\mathrm{1}×−\mathrm{5}<\mathrm{0} \\ $$$${hence}\:{the}\:{root}\:{lies}\:{btn}\:\mathrm{0}<{x}<\mathrm{1} \\ $$$$ \\ $$
Answered by Spillover last updated on 15/Jan/23
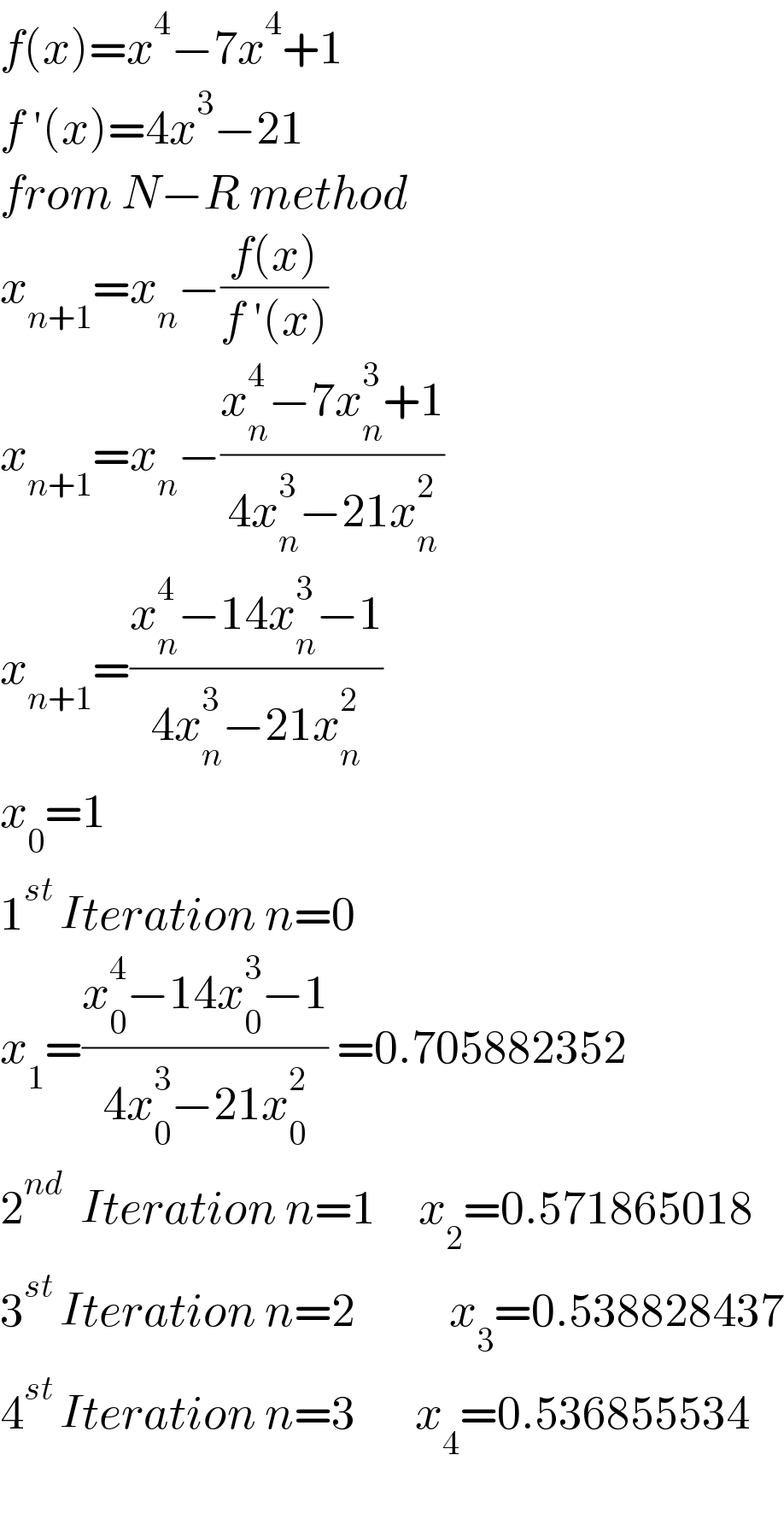
$${f}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{7}{x}^{\mathrm{4}} +\mathrm{1} \\ $$$${f}\:'\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} −\mathrm{21} \\ $$$${from}\:{N}−{R}\:{method} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{{f}\left({x}\right)}{{f}\:'\left({x}\right)} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{{x}_{{n}} ^{\mathrm{4}} −\mathrm{7}{x}_{{n}} ^{\mathrm{3}} +\mathrm{1}}{\mathrm{4}{x}_{{n}} ^{\mathrm{3}} −\mathrm{21}{x}_{{n}} ^{\mathrm{2}} } \\ $$$${x}_{{n}+\mathrm{1}} =\frac{{x}_{{n}} ^{\mathrm{4}} −\mathrm{14}{x}_{{n}} ^{\mathrm{3}} −\mathrm{1}}{\mathrm{4}{x}_{{n}} ^{\mathrm{3}} −\mathrm{21}{x}_{{n}} ^{\mathrm{2}} } \\ $$$${x}_{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{1}^{{st}\:} {Iteration}\:{n}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{{x}_{\mathrm{0}} ^{\mathrm{4}} −\mathrm{14}{x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{1}}{\mathrm{4}{x}_{\mathrm{0}} ^{\mathrm{3}} −\mathrm{21}{x}_{\mathrm{0}} ^{\mathrm{2}} }\:=\mathrm{0}.\mathrm{705882352} \\ $$$$\mathrm{2}^{{nd}} \:\:{Iteration}\:{n}=\mathrm{1}\:\:\:\:\:{x}_{\mathrm{2}} =\mathrm{0}.\mathrm{571865018} \\ $$$$\mathrm{3}^{{st}\:} {Iteration}\:{n}=\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:{x}_{\mathrm{3}} =\mathrm{0}.\mathrm{538828437} \\ $$$$\mathrm{4}^{{st}\:} {Iteration}\:{n}=\mathrm{3}\:\:\:\:\:\:\:{x}_{\mathrm{4}} =\mathrm{0}.\mathrm{536855534} \\ $$$$ \\ $$
