
Question Number 178837 by ARUNG_Brandon_MBU last updated on 22/Oct/22
Answered by HeferH last updated on 22/Oct/22

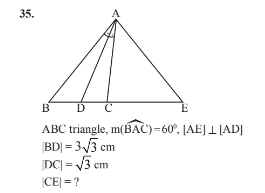
$$\mathrm{2}\sqrt{\mathrm{3}}\:? \\ $$
Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22
It's among the options.
Commented by HeferH last updated on 22/Oct/22
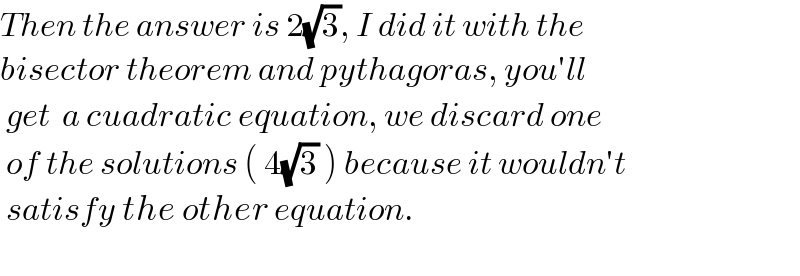
$${Then}\:{the}\:{answer}\:{is}\:\mathrm{2}\sqrt{\mathrm{3}},\:{I}\:{did}\:{it}\:{with}\:{the}\: \\ $$$${bisector}\:{theorem}\:{and}\:{pythagoras},\:{you}'{ll} \\ $$$$\:{get}\:\:{a}\:{cuadratic}\:{equation},\:{we}\:{discard}\:{one} \\ $$$$\:{of}\:{the}\:{solutions}\:\left(\:\mathrm{4}\sqrt{\mathrm{3}}\:\right)\:{because}\:{it}\:{wouldn}'{t} \\ $$$$\:{satisfy}\:{the}\:{other}\:{equation}. \\ $$$$\: \\ $$
Commented by HeferH last updated on 22/Oct/22

$${Its}\:{AD}\:{bisector}? \\ $$
Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22
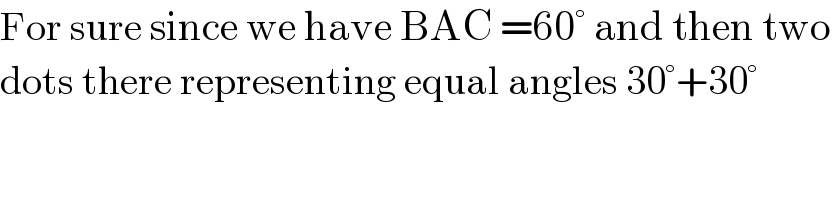
$$\mathrm{For}\:\mathrm{sure}\:\mathrm{since}\:\mathrm{we}\:\mathrm{have}\:\mathrm{BAC}\:=\mathrm{60}°\:\mathrm{and}\:\mathrm{then}\:\mathrm{two} \\ $$$$\mathrm{dots}\:\mathrm{there}\:\mathrm{representing}\:\mathrm{equal}\:\mathrm{angles}\:\mathrm{30}°+\mathrm{30}° \\ $$
Commented by HeferH last updated on 22/Oct/22
Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22
Thank you !
Commented by HeferH last updated on 22/Oct/22

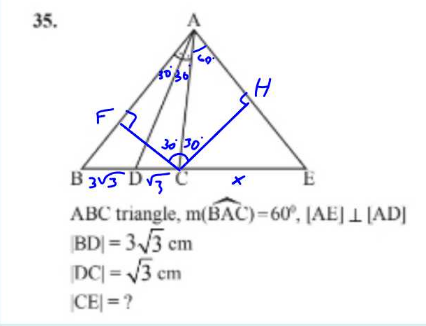
$$\:{let}\:{AB}\:=\:{a},\:{AC}=\:{c}\:,\:{AE}\:=\:{b} \\ $$$$\:\mathrm{1}.\:{Since}\:{AD}\:{is}\:{bisector}: \\ $$$$\:\frac{{a}}{\mathrm{3}\sqrt{\mathrm{3}}}\:=\:\frac{{c}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:{a}\sqrt{\mathrm{3}}\:=\:\mathrm{3}\sqrt{\mathrm{3}}\:{c} \\ $$$$\:{a}=\mathrm{3}{c}={AB} \\ $$$$\: \\ $$$$\:\mathrm{2}.\:\bigtriangleup{AFC}\:{has}\:{a}\:{hipotenuse}\:{of}\:{c},\:{then}\: \\ $$$$\:{AF}=\frac{{c}}{\mathrm{2}}\:;\:{FC}=\:\frac{{c}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\: \\ $$$$\:\mathrm{3}.\:{FB}=\:{AB}−{AF}\:\Rightarrow\:{FB}=\:\frac{\mathrm{5}{c}}{\mathrm{2}} \\ $$$$\:{FB}^{\mathrm{2}} \:+\:{FC}^{\mathrm{2}} =\:\left(\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:\frac{\mathrm{25}{c}^{\mathrm{2}} }{\mathrm{4}}\:+\:\frac{\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{4}}=\:\mathrm{48} \\ $$$$\:{c}=\:\sqrt{\frac{\mathrm{48}\centerdot\mathrm{4}}{\mathrm{28}}}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{7}}}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{21}}}{\mathrm{7}} \\ $$$$\:\mathrm{4}.\:\bigtriangleup{AHC}\:\cong\:\bigtriangleup{AFC}\:\left({Angle};\:{side};\:{Angle}\right) \\ $$$$\:{AH}\:=\:\frac{{c}}{\mathrm{2}};\:\:{CH}=\:\frac{{c}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\mathrm{5}.\:\:{AC}\:{is}\:{also}\:{bisector} \\ $$$$\:\:\frac{\mathrm{3}{c}}{\mathrm{4}\sqrt{\mathrm{3}}}\:=\:\frac{{b}}{{x}} \\ $$$$\:{b}\:=\:\:\frac{\mathrm{3}{x}\sqrt{\mathrm{7}}}{\mathrm{7}}\: \\ $$$$\:\mathrm{6}.\:{HE}\:=\:{AE}\:−\:{AH}\:=\:{b}−\frac{{c}}{\mathrm{2}} \\ $$$$\:{CH}^{\mathrm{2}} \:+\:{HE}^{\mathrm{2}} ={x}^{\mathrm{2}} \\ $$$$\:\frac{\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{4}}\:+\:\left({b}−\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} \\ $$$$\:\frac{\mathrm{3}}{\mathrm{4}}\centerdot\:\left(\frac{\mathrm{4}\sqrt{\mathrm{21}}}{\mathrm{7}}\right)^{\mathrm{2}} \:+\:\left(\frac{\mathrm{3}{x}\sqrt{\mathrm{7}}\:−\:\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{7}}\right)^{\mathrm{2}} =\:{x}^{\mathrm{2}} \\ $$$$\:\frac{\mathrm{36}}{\mathrm{7}}\:+\:\frac{\left(\mathrm{3}{x}\sqrt{\mathrm{7}}\:−\mathrm{2}\sqrt{\mathrm{21}}\right)^{\mathrm{2}} }{\mathrm{49}}\:={x}^{\mathrm{2}} \\ $$$$\:\mathrm{7}\centerdot\mathrm{36}\:+\:\left(\mathrm{3}{x}\sqrt{\mathrm{7}}\:−\mathrm{2}\sqrt{\mathrm{21}}\:\right)^{\mathrm{2}} =\:\mathrm{49}{x}^{\mathrm{2}} \\ $$$$\:\mathrm{14}{x}^{\mathrm{2}} \:−\:\mathrm{84}{x}\sqrt{\mathrm{3}}\:+\:\:\mathrm{336}=\mathrm{0} \\ $$$$\:{x}_{\mathrm{1}} =\:\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\:{x}_{\mathrm{2}} =\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\: \\ $$
Commented by HeferH last updated on 22/Oct/22
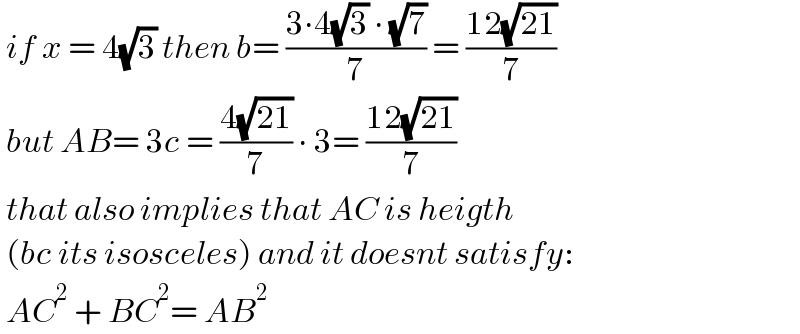
$$\:{if}\:{x}\:=\:\mathrm{4}\sqrt{\mathrm{3}}\:{then}\:{b}=\:\frac{\mathrm{3}\centerdot\mathrm{4}\sqrt{\mathrm{3}}\:\centerdot\:\sqrt{\mathrm{7}}}{\mathrm{7}}\:=\:\frac{\mathrm{12}\sqrt{\mathrm{21}}}{\mathrm{7}}\:\: \\ $$$$\:{but}\:{AB}=\:\mathrm{3}{c}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{21}}}{\mathrm{7}}\:\centerdot\:\mathrm{3}=\:\frac{\mathrm{12}\sqrt{\mathrm{21}}}{\mathrm{7}} \\ $$$$\:{that}\:{also}\:{implies}\:{that}\:{AC}\:{is}\:{heigth} \\ $$$$\:\left({bc}\:{its}\:{isosceles}\right)\:{and}\:{it}\:{doesnt}\:{satisfy}: \\ $$$$\:{AC}^{\mathrm{2}} \:+\:{BC}^{\mathrm{2}} =\:{AB}^{\mathrm{2}} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22
����
