
Question Number 178751 by mathlove last updated on 21/Oct/22
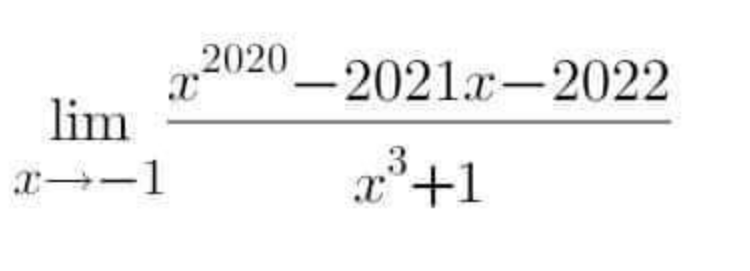
Answered by cortano1 last updated on 21/Oct/22
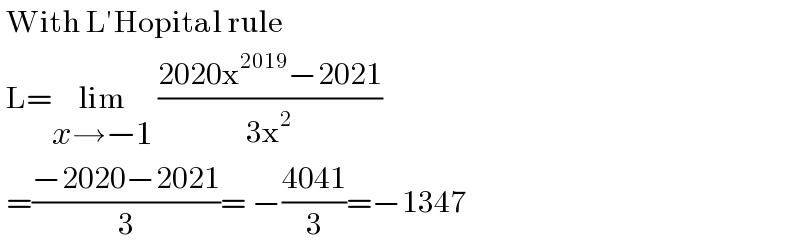
$$\:\mathrm{With}\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{rule} \\ $$$$\:\mathrm{L}=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2020x}^{\mathrm{2019}} −\mathrm{2021}}{\mathrm{3x}^{\mathrm{2}} } \\ $$$$\:=\frac{−\mathrm{2020}−\mathrm{2021}}{\mathrm{3}}=\:−\frac{\mathrm{4041}}{\mathrm{3}}=−\mathrm{1347} \\ $$
Commented by mathlove last updated on 21/Oct/22
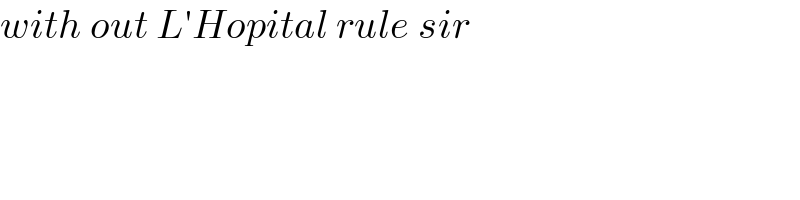
$${with}\:{out}\:{L}'{Hopital}\:{rule}\:{sir} \\ $$
Answered by cortano1 last updated on 21/Oct/22
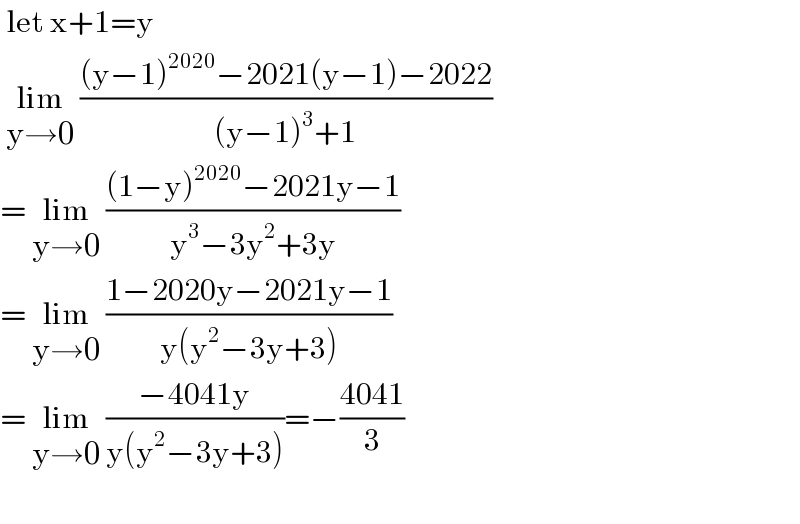
$$\:\mathrm{let}\:\mathrm{x}+\mathrm{1}=\mathrm{y} \\ $$$$\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2020}} −\mathrm{2021}\left(\mathrm{y}−\mathrm{1}\right)−\mathrm{2022}}{\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{1}} \\ $$$$=\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\mathrm{y}\right)^{\mathrm{2020}} −\mathrm{2021y}−\mathrm{1}}{\mathrm{y}^{\mathrm{3}} −\mathrm{3y}^{\mathrm{2}} +\mathrm{3y}} \\ $$$$=\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{2020y}−\mathrm{2021y}−\mathrm{1}}{\mathrm{y}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{3y}+\mathrm{3}\right)} \\ $$$$=\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{4041y}}{\mathrm{y}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{3y}+\mathrm{3}\right)}=−\frac{\mathrm{4041}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by mathlove last updated on 22/Oct/22

$${thank}\:{sir} \\ $$
Answered by kapoorshah last updated on 21/Oct/22

$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\:−\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2020}} \:−\:\mathrm{1}\:−\:\mathrm{2021}{x}\:−\:\mathrm{2021}\:\:}{\left({x}\:+\:\mathrm{1}\right)\left(\:{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:=\underset{{x}\rightarrow\:−\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\:{x}\:+\:\mathrm{1}\right)\left({x}^{\mathrm{1019}} \:−\:{x}^{\mathrm{1018}} \:+\:{x}^{\mathrm{1017}} \:−\:{x}^{\mathrm{1016}} \:+\:.....\:+\:{x}\:−\:\mathrm{1}\right)\:−\:\mathrm{2021}\left({x}\:+\:\mathrm{1}\right)\:\:}{\left({x}\:+\:\mathrm{1}\right)\left(\:{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{1}\right)}\: \\ $$$$\:\:\:\:\:\:=\underset{{x}\rightarrow\:−\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{1019}} \:−\:{x}^{\mathrm{1018}} \:+\:{x}^{\mathrm{1017}} \:−\:{x}^{\mathrm{1016}} \:+\:.....\:+\:{x}\:−\:\mathrm{1}\:−\:\mathrm{2021}}{\:{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{1}}\: \\ $$$$\:\:\:\:\:\:=\:\frac{−\mathrm{1}\:−\:\mathrm{1}\:−\:\mathrm{1}\:−\:\mathrm{1}\:−\:.....\:−\:\mathrm{1}\:−\:\mathrm{1}\:−\:\mathrm{2021}}{\:\mathrm{1}\:+\:\mathrm{1}\:+\:\mathrm{1}}\: \\ $$$$\:\:\:\:\:\:=\:\frac{−\:\mathrm{2020}\:−\:\mathrm{2021}}{\:\mathrm{3}}\: \\ $$$$\:\:\:\:\:\:=\:−\:\mathrm{1347} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathlove last updated on 22/Oct/22

$${thanks}\:{sir} \\ $$
