
Question Number 178686 by greougoury555 last updated on 20/Oct/22
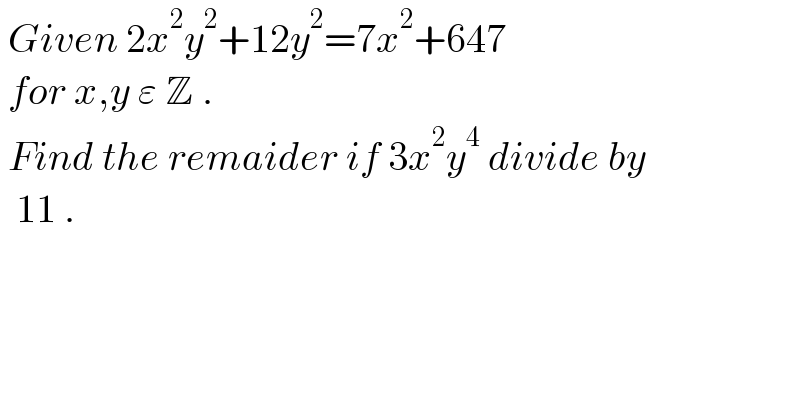
$$\:{Given}\:\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{12}{y}^{\mathrm{2}} =\mathrm{7}{x}^{\mathrm{2}} +\mathrm{647}\: \\ $$$$\:{for}\:{x},{y}\:\varepsilon\:\mathbb{Z}\:. \\ $$$$\:{Find}\:{the}\:{remaider}\:{if}\:\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{4}} \:{divide}\:{by} \\ $$$$\:\:\mathrm{11}\:. \\ $$
Answered by Rasheed.Sindhi last updated on 20/Oct/22

$$\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{12}{y}^{\mathrm{2}} =\mathrm{7}{x}^{\mathrm{2}} +\mathrm{647} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{6}\right)=\mathrm{7}\left({x}^{\mathrm{2}} +\mathrm{6}\right)+\mathrm{605} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{6}\right)−\mathrm{7}\left({x}^{\mathrm{2}} +\mathrm{6}\right)=\mathrm{605} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{6}\right)\left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}\right)=\mathrm{5}×\mathrm{11}^{\mathrm{2}} ......{A} \\ $$$${Possible}\:{values}\:{for}\:{x}^{\mathrm{2}} +\mathrm{6}: \\ $$$$\mathrm{1},\mathrm{5},\mathrm{11},\mathrm{121},\mathrm{55},\mathrm{605},−\mathrm{1},−\mathrm{5},−\mathrm{11},−\mathrm{121},−\mathrm{55},−\mathrm{605} \\ $$$${Possible}\:{values}\:{for}\:{x}^{\mathrm{2}} \\ $$$$\overset{×} {−\mathrm{5}},\overset{×} {−\mathrm{1}},\overset{×} {\mathrm{5}},\overset{×} {\mathrm{115}},\:\:\begin{array}{|c|}{\mathrm{49}}\\\hline\end{array}^{\checkmark} ,\overset{×} {\mathrm{599}},\overset{×} {−\mathrm{7}},\overset{×} {−\mathrm{11}},\overset{×} {−\mathrm{17}},\overset{×} {−\mathrm{127}},\overset{×} {−\mathrm{61}},\overset{×} {−\mathrm{611}} \\ $$$$\because\:{x}\in\mathbb{Z}\:\:\:\:\therefore\:\:\:{x}^{\mathrm{2}} =\mathrm{49}\Rightarrow{x}=\pm\mathrm{7} \\ $$$${If}\:{x}^{\mathrm{2}} +\mathrm{6}=\left(\pm\mathrm{7}\right)^{\mathrm{2}} +\mathrm{6}=\mathrm{55}\:{then}\:{from}\:{A} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}=\mathrm{605}/\mathrm{55}=\mathrm{11} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} =\mathrm{18}\Rightarrow{y}=\pm\mathrm{3} \\ $$$$\: \\ $$$$\left({x},{y}\right)=\left(\pm\mathrm{7},\pm\mathrm{3}\right)\:{or}\:\left(\pm\mathrm{7},\mp\mathrm{3}\right) \\ $$$$\:\:\:\:\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{4}} =\mathrm{3}\left(\pm\mathrm{7}\right)^{\mathrm{2}} \left(\pm\mathrm{3}\right)^{\mathrm{4}} =\mathrm{3}\left(\pm\mathrm{7}\right)^{\mathrm{2}} \left(\mp\mathrm{3}\right)^{\mathrm{4}} =\mathrm{11907} \\ $$$$\:\:\:\:\mathrm{11907}\:\left({mod}\:\mathrm{11}\right)=\begin{array}{|c|}{\mathrm{5}}\\\hline\end{array} \\ $$
Commented by cortano1 last updated on 21/Oct/22

$$\:\mathrm{typo}\:\Rightarrow\mathrm{2y}^{\mathrm{2}} =\mathrm{18}\:;\:\mathrm{y}=\pm\:\mathrm{3} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\:\left(\pm\mathrm{7}\:,\pm\mathrm{3}\right) \\ $$$$\mathrm{then}\:\mathrm{3x}^{\mathrm{2}} \mathrm{y}^{\mathrm{4}} =\mathrm{3}×\mathrm{49}×\mathrm{81}=\mathrm{11907} \\ $$$$\:\mathrm{11907}\:=\:\mathrm{1082}×\mathrm{11}+\mathrm{5}=\mathrm{5}\left(\mathrm{mod}\:\mathrm{11}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 20/Oct/22
$$\mathcal{T}{hank}\:{you}\:{sir},{I}'{ve}\:\:{corrected}\:{now}. \\ $$
Answered by greougoury555 last updated on 21/Oct/22
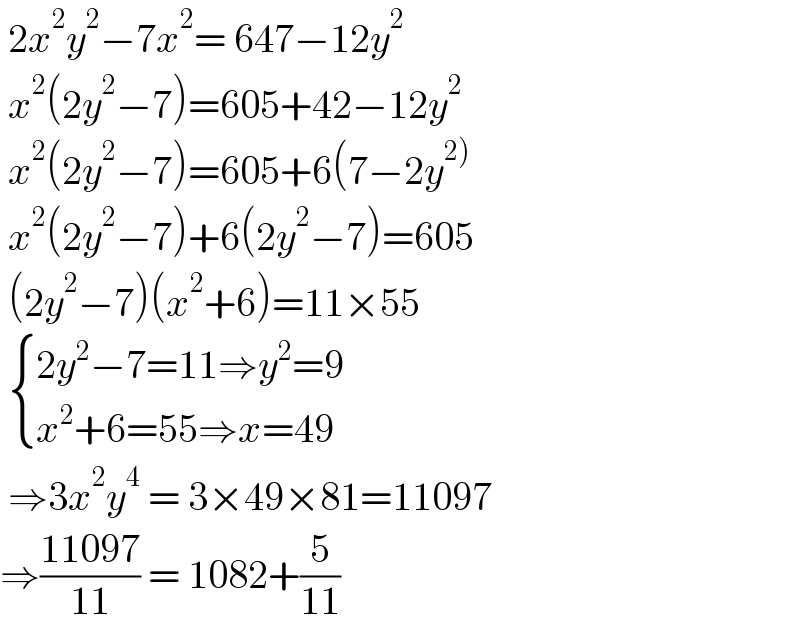
$$\:\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{7}{x}^{\mathrm{2}} =\:\mathrm{647}−\mathrm{12}{y}^{\mathrm{2}} \\ $$$$\:{x}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}\right)=\mathrm{605}+\mathrm{42}−\mathrm{12}{y}^{\mathrm{2}} \\ $$$$\:{x}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}\right)=\mathrm{605}+\mathrm{6}\left(\mathrm{7}−\mathrm{2}{y}^{\left.\mathrm{2}\right)} \right. \\ $$$$\:{x}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}\right)+\mathrm{6}\left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}\right)=\mathrm{605} \\ $$$$\:\left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}\right)\left({x}^{\mathrm{2}} +\mathrm{6}\right)=\mathrm{11}×\mathrm{55} \\ $$$$\:\begin{cases}{\mathrm{2}{y}^{\mathrm{2}} −\mathrm{7}=\mathrm{11}\Rightarrow{y}^{\mathrm{2}} =\mathrm{9}}\\{{x}^{\mathrm{2}} +\mathrm{6}=\mathrm{55}\Rightarrow{x}=\mathrm{49}}\end{cases} \\ $$$$\:\Rightarrow\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{4}} \:=\:\mathrm{3}×\mathrm{49}×\mathrm{81}=\mathrm{11097} \\ $$$$\Rightarrow\frac{\mathrm{11097}}{\mathrm{11}}\:=\:\mathrm{1082}+\frac{\mathrm{5}}{\mathrm{11}} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Oct/22

$$\mathcal{T}{ypo}:\:\mathrm{3}×\mathrm{49}×\mathrm{81}=\mathrm{11907} \\ $$
