
Question Number 178673 by Tawa11 last updated on 20/Oct/22
Answered by mr W last updated on 20/Oct/22
![I=((mr^2 )/2)+mr^2 =((3mr^2 )/2) ((Iω^2 )/2)=mgLsin θ ω=(1/r)(√((2gLsin θ)/(3/2)))=(2/r)(√((gLsin θ)/3))=(2/(0.1))(√((9.81×6×sin 30°)/3))=62.64 rad/s v=ωr=6.264 m/s t=(d/(v cos θ)) H=v sin θ t+((gt^2 )/2) H=v sin θ×(d/(v cos θ))+(g/2)×(d^2 /(v^2 cos^2 θ)) ⇒((g(1+tan^2 θ))/(2v^2 ))d^2 +tan θ d−H=0 d=(v^2 /(g(1+tan^2 θ)))[−tan θ+(√(tan^2 θ+((2gH(1+tan^2 θ))/v^2 )))] d=((6.264^2 )/(9.81(1+(1/3))))[−(1/( (√3)))+(√((1/3)+((2×9.81×5(1+(1/3)))/(6.264^2 ))))]≈4.01 m](Q178689.png)
$${I}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}+{mr}^{\mathrm{2}} =\frac{\mathrm{3}{mr}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{I}\omega^{\mathrm{2}} }{\mathrm{2}}={mgL}\mathrm{sin}\:\theta \\ $$$$\omega=\frac{\mathrm{1}}{{r}}\sqrt{\frac{\mathrm{2}{gL}\mathrm{sin}\:\theta}{\frac{\mathrm{3}}{\mathrm{2}}}}=\frac{\mathrm{2}}{{r}}\sqrt{\frac{{gL}\mathrm{sin}\:\theta}{\mathrm{3}}}=\frac{\mathrm{2}}{\mathrm{0}.\mathrm{1}}\sqrt{\frac{\mathrm{9}.\mathrm{81}×\mathrm{6}×\mathrm{sin}\:\mathrm{30}°}{\mathrm{3}}}=\mathrm{62}.\mathrm{64}\:{rad}/{s} \\ $$$${v}=\omega{r}=\mathrm{6}.\mathrm{264}\:{m}/{s} \\ $$$$ \\ $$$${t}=\frac{{d}}{{v}\:\mathrm{cos}\:\theta} \\ $$$${H}={v}\:\mathrm{sin}\:\theta\:{t}+\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${H}={v}\:\mathrm{sin}\:\theta×\frac{{d}}{{v}\:\mathrm{cos}\:\theta}+\frac{{g}}{\mathrm{2}}×\frac{{d}^{\mathrm{2}} }{{v}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow\frac{{g}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{v}^{\mathrm{2}} }{d}^{\mathrm{2}} +\mathrm{tan}\:\theta\:{d}−{H}=\mathrm{0} \\ $$$${d}=\frac{{v}^{\mathrm{2}} }{{g}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}\left[−\mathrm{tan}\:\theta+\sqrt{\mathrm{tan}^{\mathrm{2}} \:\theta+\frac{\mathrm{2}{gH}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{{v}^{\mathrm{2}} }}\right] \\ $$$${d}=\frac{\mathrm{6}.\mathrm{264}^{\mathrm{2}} }{\mathrm{9}.\mathrm{81}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)}\left[−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}×\mathrm{9}.\mathrm{81}×\mathrm{5}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{6}.\mathrm{264}^{\mathrm{2}} }}\right]\approx\mathrm{4}.\mathrm{01}\:{m} \\ $$
Commented by Tawa11 last updated on 20/Oct/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by Acem last updated on 20/Oct/22

$$ \\ $$$$\:{Here}\:\mu=\:\mathrm{0}\:{and}\:{without}\:{friction}\:{the}\:{cylinder}\:{won}'{t} \\ $$$$\:{roll}\:{but}\:{will}\:{slipps}...\:{anyway}\:{it}\:{seems}\:{the}\:{director} \\ $$$$\:{wants}\:{to}\:{roll}\:{it}\:{by}\:{force}! \\ $$$$ \\ $$$${a}\bullet\:{w}=\:\frac{\sqrt{\frac{\mathrm{2}{gL}\mathrm{sin}\:\theta}{\mathrm{1}+{c}}}}{{R}}\:=\:\mathrm{62}.\mathrm{64}\:\:{rad}.{s}^{−\mathrm{1}} \\ $$$$\:;\:{c}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:,\:{v}=\:\mathrm{6}.\mathrm{264}\:{m}.{s}^{−\mathrm{1}} \\ $$$$ \\ $$$${b}\bullet\:{v}_{\mathrm{0}} =\:\mathrm{6}.\mathrm{264}\:{m}.{s}^{−\mathrm{1}} \:\measuredangle\:\mathrm{30}^{°} \\ $$$${H}=\:{v}_{\mathrm{0}} .\mathrm{sin}\:\theta.{t}\:+\mathrm{0}.\mathrm{5}{g}.{t}^{\mathrm{2}} \\ $$$$\:\mathrm{4}.\mathrm{905}{t}^{\mathrm{2}} +\:\mathrm{3}.\mathrm{132}{t}−\:\mathrm{5}=\:\mathrm{0}\:\Rightarrow\:{t}=\:\mathrm{0}.\mathrm{739}\:{s} \\ $$$$ \\ $$$$\:{Horizontal}\:{distance}=\:{v}_{\mathrm{0}} \mathrm{cos}\:\theta.{t}=\:\mathrm{4}.\mathrm{008}\:{m} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 20/Oct/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by Acem last updated on 20/Oct/22
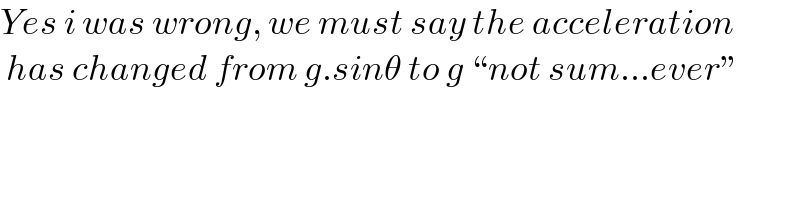
$${Yes}\:{i}\:{was}\:{wrong},\:{we}\:{must}\:{say}\:{the}\:{acceleration} \\ $$$$\:{has}\:{changed}\:{from}\:{g}.{sin}\theta\:{to}\:{g}\:``{not}\:{sum}...{ever}'' \\ $$
Commented by Acem last updated on 20/Oct/22

$${You}'{re}\:{very}\:{much}\:{welcome}...\:{let}\:{me}\:{know}\:{how} \\ $$$$\:{many}\:{cycles}\:{the}\:{cylinder}\:{did}\:{when}\:{reached}\:{the}\:{edge} \\ $$$$\:{plus}\:{the}\:{angle}\:{if}\:{any}. \\ $$$$\left(:\:{think}\:{it}\:{before}\:{starting}\:{the}\:{solve}\:=\right) \\ $$
Commented by Tawa11 last updated on 20/Oct/22
$$\mathrm{sir}\:\mathrm{mrW}\:\:\mathrm{distance}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 20/Oct/22
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
