
Question Number 17867 by Mr easymsn last updated on 11/Jul/17
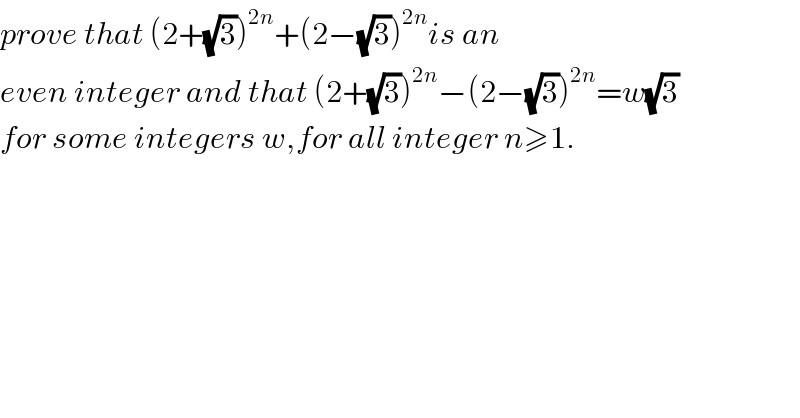
$${prove}\:{that}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}{n}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}{n}} {is}\:{an} \\ $$$${even}\:{integer}\:{and}\:{that}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}{n}} −\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}{n}} ={w}\sqrt{\mathrm{3}} \\ $$$${for}\:{some}\:{integers}\:{w},{for}\:{all}\:{integer}\:{n}\geqslant\mathrm{1}. \\ $$$$ \\ $$
Answered by alex041103 last updated on 11/Jul/17
![We expand using (a+b)^n =Σ_(k=0) ^n ((n),(k) ) a^(n−k) b^k We get (2+(√3))^(2n) + (2−(√3))^(2n) = =Σ_(k=0) ^(2n) (((2n)),(( k)) ) 2^(2n−k) ((√3))^k [1+(−1)^k ] When k≡1(mod 2) (((2n)),(( k)) ) 2^(2n−k) ((√3))^k [1+(−1)^k ]=0 That′s why k≡0(mod 2) ⇒(2+(√3))^(2n) + (2−(√3))^(2n) = =Σ_(k=0) ^n (((2n)),(( 2k)) ) 2^(2n−2k) (3^(1/2) )^(2k) ×2 =2Σ_(k=0) ^n (((2n)),(( 2k)) ) 2^(2n−2k) ×3^k It′s easy to show that Σ_(k=0) ^n (((2n)),(( 2k)) ) 2^(2n−2k) ×3^k ∈ N ⇒(((2+(√3))^(2n) +(2−(√3))^(2n) )/2)∈N The same procedure works for the next statement (2+(√3))^(2n) − (2−(√3))^(2n) = =Σ_(k=0) ^(2n) (((2n)),(( k)) ) 2^(2n−k) ((√3))^k [1+(−1)^(k+1) ] Then we substitute k=2t+1 and (2+(√3))^(2n) − (2−(√3))^(2n) = =Σ_(k=0) ^(n−1) ((( 2n)),(( 2k+1)) ) 2^(2n−2k) ((√3))3^k =(√3)Σ_(k=0) ^(n−1) ((( 2n)),(( 2k+1)) ) 2^(2n−2k) 3^k ⇒(2+(√3))^(2n) − (2−(√3))^(2n) =w(√3), w∈N](Q17868.png)
$$\mathrm{We}\:\mathrm{expand}\:\mathrm{using} \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\:\mathrm{a}^{\mathrm{n}−\mathrm{k}} \:\mathrm{b}^{\mathrm{k}} \\ $$$$\mathrm{We}\:\mathrm{get} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} \:+\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} = \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{k}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{k}} \left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \left[\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{k}} \right] \\ $$$$\mathrm{When}\:\mathrm{k}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$$\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{k}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{k}} \left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \left[\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{k}} \right]=\mathrm{0} \\ $$$$\mathrm{That}'\mathrm{s}\:\mathrm{why}\:\mathrm{k}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right)\: \\ $$$$\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} \:+\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} = \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{2k}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{2k}} \left(\mathrm{3}^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{2k}} ×\mathrm{2} \\ $$$$=\mathrm{2}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{2k}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{2k}} ×\mathrm{3}^{\mathrm{k}} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{2k}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{2k}} ×\mathrm{3}^{\mathrm{k}} \:\in\:\mathbb{N} \\ $$$$\Rightarrow\frac{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} }{\mathrm{2}}\in\mathbb{N} \\ $$$$\mathrm{The}\:\mathrm{same}\:\mathrm{procedure}\:\mathrm{works}\:\mathrm{for}\:\mathrm{the}\:\mathrm{next}\:\mathrm{statement} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} \:−\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} = \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{k}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{k}} \left(\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \left[\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} \right] \\ $$$$\mathrm{Then}\:\mathrm{we}\:\mathrm{substitute}\:\mathrm{k}=\mathrm{2t}+\mathrm{1}\:\mathrm{and} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} \:−\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} = \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\:\:\:\:\mathrm{2n}}\\{\:\mathrm{2k}+\mathrm{1}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{2k}} \left(\sqrt{\mathrm{3}}\right)\mathrm{3}^{\mathrm{k}} \\ $$$$=\sqrt{\mathrm{3}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\:\:\:\:\mathrm{2n}}\\{\:\mathrm{2k}+\mathrm{1}}\end{pmatrix}\:\mathrm{2}^{\mathrm{2n}−\mathrm{2k}} \mathrm{3}^{\mathrm{k}} \\ $$$$\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} \:−\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2n}} =\mathrm{w}\sqrt{\mathrm{3}},\:\mathrm{w}\in\mathbb{N} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by alex041103 last updated on 12/Jul/17
$${Is}\:{there}\:{a}\:{problem},\:{sir}? \\ $$
