
Previous in Relation and Functions Next in Relation and Functions
Question Number 178635 by infinityaction last updated on 19/Oct/22
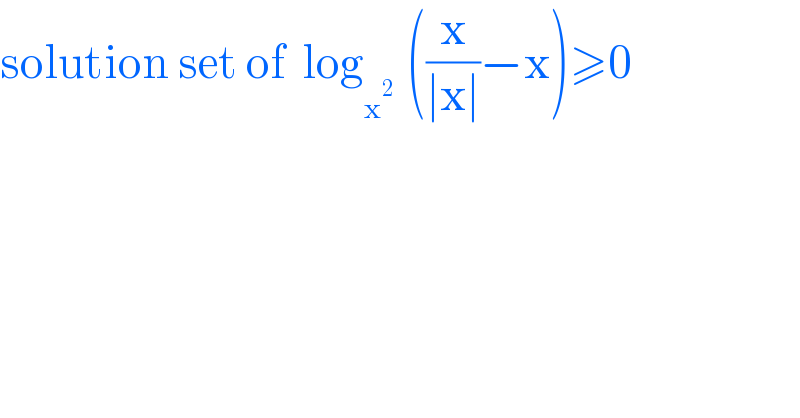
$$\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\:\mathrm{log}_{\mathrm{x}^{\mathrm{2}\:\:\:} } \left(\frac{\mathrm{x}}{\mid\mathrm{x}\mid}−\mathrm{x}\right)\geqslant\mathrm{0} \\ $$
Commented by Frix last updated on 19/Oct/22

$${x}\leqslant−\mathrm{2}\vee\mathrm{0}<{x}<\mathrm{1} \\ $$
Commented by infinityaction last updated on 20/Oct/22

$${sir}\:{solution} \\ $$
Answered by mr W last updated on 20/Oct/22
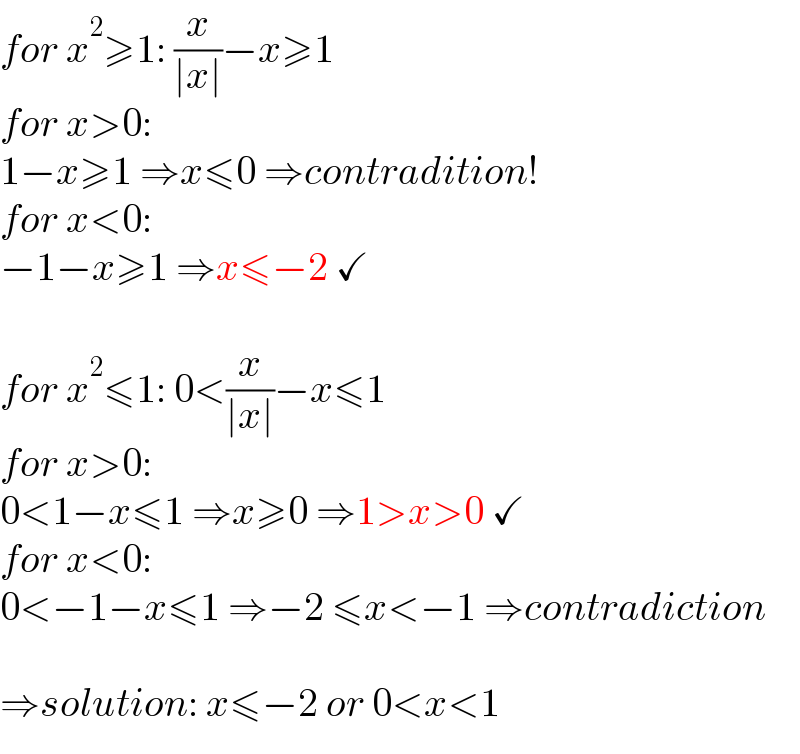
$${for}\:{x}^{\mathrm{2}} \geqslant\mathrm{1}:\:\frac{{x}}{\mid{x}\mid}−{x}\geqslant\mathrm{1} \\ $$$${for}\:{x}>\mathrm{0}: \\ $$$$\mathrm{1}−{x}\geqslant\mathrm{1}\:\Rightarrow{x}\leqslant\mathrm{0}\:\Rightarrow{contradition}! \\ $$$${for}\:{x}<\mathrm{0}: \\ $$$$−\mathrm{1}−{x}\geqslant\mathrm{1}\:\Rightarrow{x}\leqslant−\mathrm{2}\:\checkmark \\ $$$$ \\ $$$${for}\:{x}^{\mathrm{2}} \leqslant\mathrm{1}:\:\mathrm{0}<\frac{{x}}{\mid{x}\mid}−{x}\leqslant\mathrm{1} \\ $$$${for}\:{x}>\mathrm{0}: \\ $$$$\mathrm{0}<\mathrm{1}−{x}\leqslant\mathrm{1}\:\Rightarrow{x}\geqslant\mathrm{0}\:\Rightarrow\mathrm{1}>{x}>\mathrm{0}\:\checkmark \\ $$$${for}\:{x}<\mathrm{0}: \\ $$$$\mathrm{0}<−\mathrm{1}−{x}\leqslant\mathrm{1}\:\Rightarrow−\mathrm{2}\:\leqslant{x}<−\mathrm{1}\:\Rightarrow{contradiction} \\ $$$$ \\ $$$$\Rightarrow{solution}:\:{x}\leqslant−\mathrm{2}\:{or}\:\mathrm{0}<{x}<\mathrm{1} \\ $$
Commented by infinityaction last updated on 21/Oct/22

$${thank}\:{you}\:{sir} \\ $$
