
Question Number 178612 by Acem last updated on 19/Oct/22
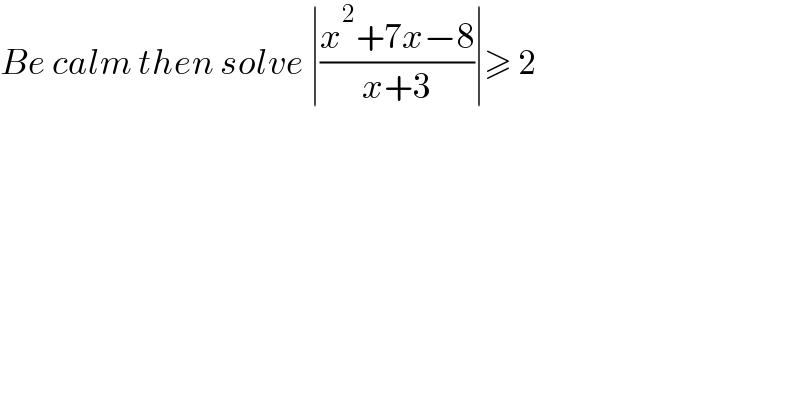
$${Be}\:{calm}\:{then}\:{solve}\:\mid\frac{{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{8}}{{x}+\mathrm{3}}\mid\geqslant\:\mathrm{2} \\ $$
Answered by cortano1 last updated on 19/Oct/22
(x−2)≥0 (x+((9+(√(89)))/2))(x+(((9−(√(89)))/2)))(x+7)(x−2)≥0](Q178613.png)
$$\:\mathrm{x}\neq−\mathrm{3} \\ $$$$\:\mid\mathrm{x}^{\mathrm{2}} +\mathrm{7x}−\mathrm{8}\mid\geqslant\mid\mathrm{2x}+\mathrm{6}\mid \\ $$$$\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{7x}−\mathrm{8}+\mathrm{2x}+\mathrm{6}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{7x}−\mathrm{8}−\mathrm{2x}−\mathrm{6}\right)\geqslant\mathrm{0} \\ $$$$\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9x}−\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{14}\right)\geqslant\mathrm{0} \\ $$$$\:\:\left[\left(\mathrm{x}+\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{89}}{\mathrm{4}}−\right]\left(\mathrm{x}+\mathrm{7}\right)\left(\mathrm{x}−\mathrm{2}\right)\geqslant\mathrm{0} \\ $$$$\:\left(\mathrm{x}+\frac{\mathrm{9}+\sqrt{\mathrm{89}}}{\mathrm{2}}\right)\left(\mathrm{x}+\left(\frac{\mathrm{9}−\sqrt{\mathrm{89}}}{\mathrm{2}}\right)\right)\left(\mathrm{x}+\mathrm{7}\right)\left(\mathrm{x}−\mathrm{2}\right)\geqslant\mathrm{0} \\ $$
Commented by Acem last updated on 19/Oct/22
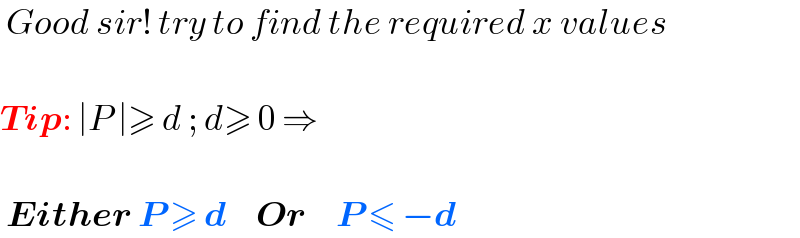
$$\:{Good}\:{sir}!\:{try}\:{to}\:{find}\:{the}\:{required}\:{x}\:{values} \\ $$$$ \\ $$$$\boldsymbol{{Tip}}:\:\mid{P}\:\mid\geqslant\:{d}\:;\:{d}\geqslant\:\mathrm{0}\:\Rightarrow \\ $$$$ \\ $$$$\:\boldsymbol{{Either}}\:\boldsymbol{{P}}\:\geqslant\:\boldsymbol{{d}}\:\:\:\:\:\boldsymbol{{Or}}\:\:\:\:\:\boldsymbol{{P}}\:\leqslant\:−\boldsymbol{{d}} \\ $$
Commented by cortano1 last updated on 19/Oct/22

$$\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{try}\:\mathrm{it} \\ $$
Commented by Acem last updated on 19/Oct/22

$${Ok}\:{friend},\:{you}\:{can}\:{check}\:{it}\:{below} \\ $$
Answered by Acem last updated on 19/Oct/22
![Either ((x^2 +7x−8)/(x+3))≥ 2 ∣_A Or ((x^2 +7x−8)/(x+3))≤ −2 ∣_B A: (((x−2)(x+1))/(x+3))≥ 0 x −∞ −7 −3 2 +∞ (x−2)(x+1) + 0 − − 0 + x+3 − − 0 + + Frac. − 0 + ∥ − 0 + Either x∈ [−7, −3[ ∪ [2, +∞[ B: (((x+(9/2))^2 −((89)/4))/(x+3))≤ 0 x= ((−9− (√(89)))/2) ≅ −9.21 or x= ((−9+ (√(89)))/2) ≅ 0.21 x −∞ x_1 −3 x_2 +∞ (x−2)(x+1) + 0 − − 0 + x+3 − − 0 + + Frac. − 0 + ∥ − 0 + Or x∈ ]−∞, ((−9− (√(89)))/2) ] ∪ ]−3, ((−9+ (√(89)))/2) ]](Q178663.png)
$$ \\ $$$${Either}\:\frac{{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{8}}{{x}+\mathrm{3}}\geqslant\:\mathrm{2}\:\mid_{\boldsymbol{{A}}} \:\:\:{Or}\:\:\:\:\frac{{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{8}}{{x}+\mathrm{3}}\leqslant\:−\mathrm{2}\:\mid_{\boldsymbol{{B}}} \\ $$$$ \\ $$$$\boldsymbol{{A}}:\:\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}{{x}+\mathrm{3}}\geqslant\:\mathrm{0} \\ $$$$\:\:\:\:\:\:{x}\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:−\mathrm{7}\:\:\:\:\:\:\:\:\:\:\cancel{−\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\mathrm{0}\:\:\:\:\:+ \\ $$$$\:\:\:\:{x}+\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\mathrm{0}\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$$\:\:\:{Frac}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\mathrm{0}\:\:\:\:\:\:+\:\:\:\:\:\:\parallel\:\:\:\:\:−\:\:\:\:\mathrm{0}\:\:\:\:\:+ \\ $$$$ \\ $$$$\:{Either}\:\boldsymbol{{x}}\in\:\left[−\mathrm{7},\:−\mathrm{3}\left[\:\cup\:\left[\mathrm{2},\:+\infty\left[\right.\right.\right.\right. \\ $$$$ \\ $$$$\boldsymbol{{B}}:\:\:\frac{\left({x}+\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{89}}{\mathrm{4}}}{{x}+\mathrm{3}}\leqslant\:\mathrm{0}\: \\ $$$$\:{x}=\:\frac{−\mathrm{9}−\:\sqrt{\mathrm{89}}}{\mathrm{2}}\:\cong\:−\mathrm{9}.\mathrm{21}\:\:{or}\:{x}=\:\frac{−\mathrm{9}+\:\sqrt{\mathrm{89}}}{\mathrm{2}}\:\cong\:\mathrm{0}.\mathrm{21} \\ $$$$ \\ $$$$\:\:\:\:\:\:{x}\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:{x}_{\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\cancel{−\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:{x}_{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\mathrm{0}\:\:\:\:\:+ \\ $$$$\:\:\:\:{x}+\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\mathrm{0}\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$$\:\:\:{Frac}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\mathrm{0}\:\:\:\:\:\:\cancel{+}\:\:\:\:\:\:\parallel\:\:\:\:\:−\:\:\:\:\mathrm{0}\:\:\:\:\:\cancel{+} \\ $$$$ \\ $$$$\left.\:\left.{O}\left.{r}\left.\:{x}\in\:\right]−\infty,\:\frac{−\mathrm{9}−\:\sqrt{\mathrm{89}}}{\mathrm{2}}\:\right]\:\cup\:\right]−\mathrm{3},\:\frac{−\mathrm{9}+\:\sqrt{\mathrm{89}}}{\mathrm{2}}\:\right] \\ $$$$ \\ $$
