
Question Number 178553 by Acem last updated on 18/Oct/22
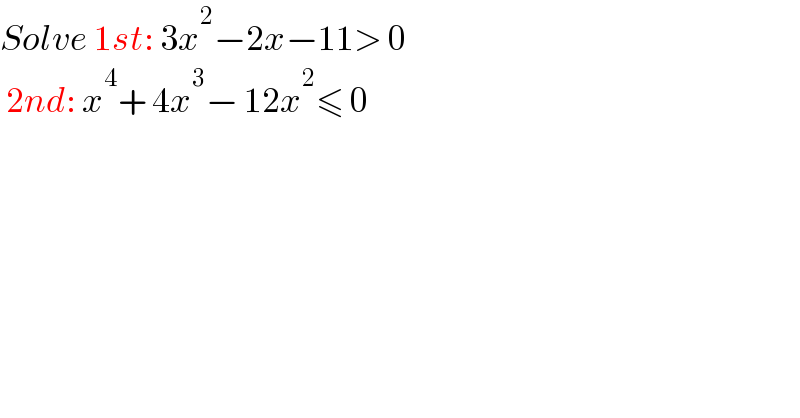
$${Solve}\:\mathrm{1}{st}:\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{11}>\:\mathrm{0} \\ $$ $$\:\mathrm{2}{nd}:\:{x}^{\mathrm{4}} +\:\mathrm{4}{x}^{\mathrm{3}} −\:\mathrm{12}{x}^{\mathrm{2}} \leqslant\:\mathrm{0} \\ $$
Answered by a.lgnaoui last updated on 18/Oct/22
![1st extremums:=(((1−(√(34)))/3);((1+(√(34)))/3))⇒3x^2 −2x−11>0 ⇔x∈]−∞,((1−(√(34)))/3)[∪]((1+(√(34)))/3),+∞ 2nd extremums:(−(1+(√7) ),0,+(1+(√7) ) ⇒2x^4 +4x^3 −12x^2 ≤0 ⇔ x∈[−(1+(√7) ),−1+(√7) )]](Q178565.png)
$$\left.\mathrm{1}{st}\:\:{extremums}:=\left(\frac{\mathrm{1}−\sqrt{\mathrm{34}}}{\mathrm{3}};\frac{\mathrm{1}+\sqrt{\mathrm{34}}}{\mathrm{3}}\right)\Rightarrow\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{11}>\mathrm{0}\:\Leftrightarrow{x}\in\right]−\infty,\frac{\mathrm{1}−\sqrt{\mathrm{34}}}{\mathrm{3}}\left[\cup\right]\frac{\mathrm{1}+\sqrt{\mathrm{34}}}{\mathrm{3}},+\infty \\ $$ $$\mathrm{2}{nd}\:{extremums}:\left(−\left(\mathrm{1}+\sqrt{\mathrm{7}}\:\right),\mathrm{0},+\left(\mathrm{1}+\sqrt{\mathrm{7}}\:\right)\:\:\Rightarrow\mathrm{2}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} \leqslant\mathrm{0}\right. \\ $$ $$\left.\:\:\Leftrightarrow\:{x}\in\left[−\left(\mathrm{1}+\sqrt{\mathrm{7}}\:\right),−\mathrm{1}+\sqrt{\mathrm{7}}\:\right)\right] \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$ $$\:\:\:\:\:\:\:\:\: \\ $$
Commented byAcem last updated on 18/Oct/22
![Good Sir! the 1st is right, the 2nd is x∈ [−6, 4] try it again, maybe i′m wrong Am sorry i noted the first term as wrong it′s x^4 not 2x^4](Q178571.png)
$${Good}\:{Sir}!\:{the}\:\mathrm{1}{st}\:{is}\:{right},\:{the}\:\mathrm{2}{nd}\:{is}\:\boldsymbol{{x}}\in\:\left[−\mathrm{6},\:\mathrm{4}\right] \\ $$ $$\:{try}\:{it}\:{again},\:{maybe}\:{i}'{m}\:{wrong} \\ $$ $$ \\ $$ $${Am}\:{sorry}\:{i}\:{noted}\:{the}\:{first}\:{term}\:{as}\:{wrong} \\ $$ $$\:\boldsymbol{{it}}'\boldsymbol{{s}}\:\boldsymbol{{x}}^{\mathrm{4}} \:\:{not}\:\mathrm{2}{x}^{\mathrm{4}} \\ $$
Answered by mr W last updated on 18/Oct/22
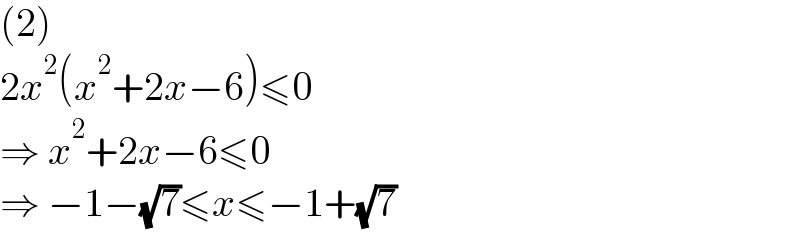
$$\left(\mathrm{2}\right) \\ $$ $$\mathrm{2}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{6}\right)\leqslant\mathrm{0} \\ $$ $$\Rightarrow\:{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{6}\leqslant\mathrm{0} \\ $$ $$\Rightarrow\:−\mathrm{1}−\sqrt{\mathrm{7}}\leqslant{x}\leqslant−\mathrm{1}+\sqrt{\mathrm{7}} \\ $$
Commented byAcem last updated on 18/Oct/22
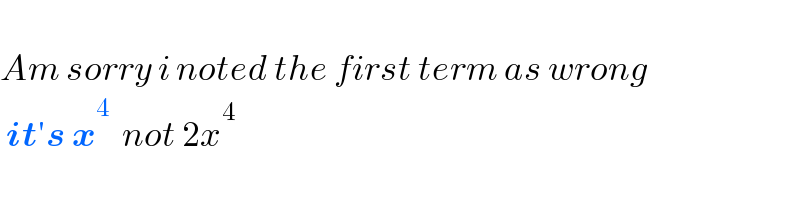
$$ \\ $$ $${Am}\:{sorry}\:{i}\:{noted}\:{the}\:{first}\:{term}\:{as}\:{wrong} \\ $$ $$\:\boldsymbol{{it}}'\boldsymbol{{s}}\:\boldsymbol{{x}}^{\mathrm{4}} \:\:{not}\:\mathrm{2}{x}^{\mathrm{4}} \\ $$
