
Question Number 178500 by infinityaction last updated on 17/Oct/22
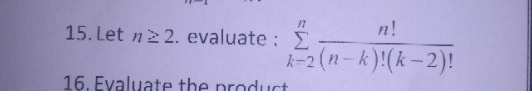
Commented by abdullahoudou last updated on 17/Oct/22
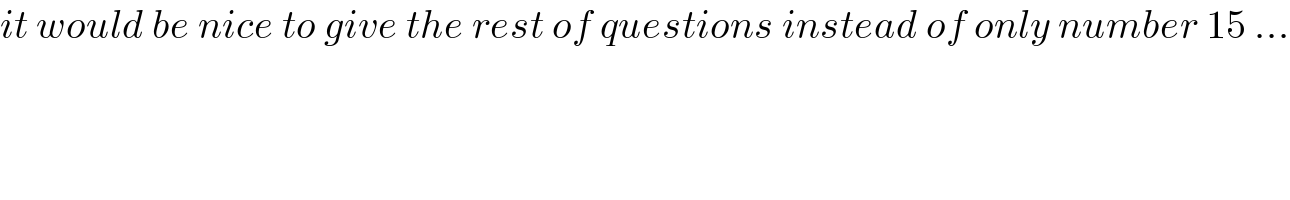
$${it}\:{would}\:{be}\:{nice}\:{to}\:{give}\:{the}\:{rest}\:{of}\:{questions}\:{instead}\:{of}\:{only}\:{number}\:\mathrm{15}\:... \\ $$
Answered by mindispower last updated on 17/Oct/22
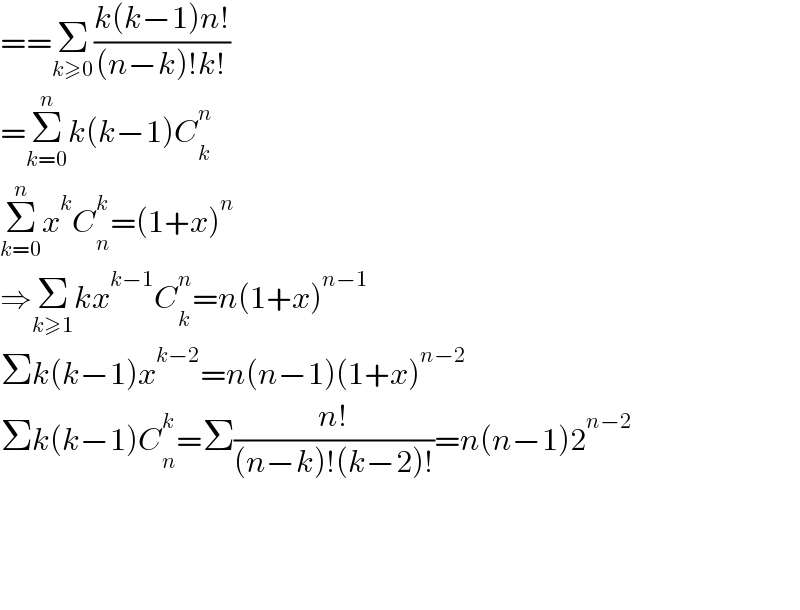
$$==\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{k}\left({k}−\mathrm{1}\right){n}!}{\left({n}−{k}\right)!{k}!} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\left({k}−\mathrm{1}\right){C}_{{k}} ^{{n}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{k}} {C}_{{n}} ^{{k}} =\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$$\Rightarrow\underset{{k}\geqslant\mathrm{1}} {\sum}{kx}^{{k}−\mathrm{1}} {C}_{{k}} ^{{n}} ={n}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} \\ $$$$\Sigma{k}\left({k}−\mathrm{1}\right){x}^{{k}−\mathrm{2}} ={n}\left({n}−\mathrm{1}\right)\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{2}} \\ $$$$\Sigma{k}\left({k}−\mathrm{1}\right){C}_{{n}} ^{{k}} =\Sigma\frac{{n}!}{\left({n}−{k}\right)!\left({k}−\mathrm{2}\right)!}={n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 17/Oct/22

$${thank}\:{you}\:{sir} \\ $$
Commented by mindispower last updated on 02/Nov/22

$${withe}\:{pleasur} \\ $$
