Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 178486 by Acem last updated on 17/Oct/22

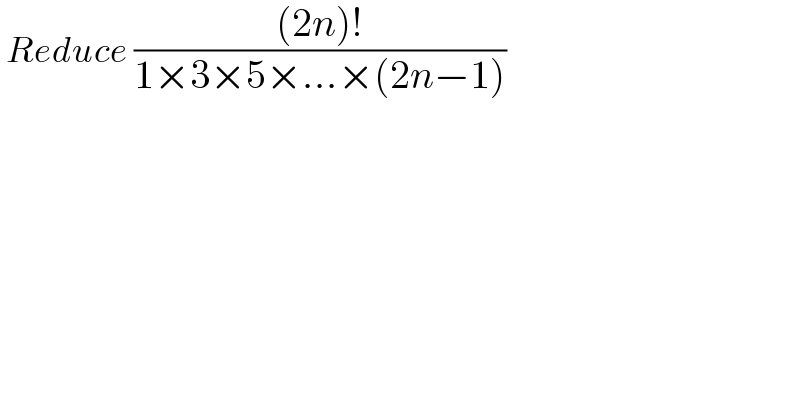
Reduce (((2n)!)/(1×3×5×...×(2n−1)))

$$\:{Reduce}\:\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{1}×\mathrm{3}×\mathrm{5}×...×\left(\mathrm{2}{n}−\mathrm{1}\right)}\: \\ $$

Answered by Rasheed.Sindhi last updated on 17/Oct/22

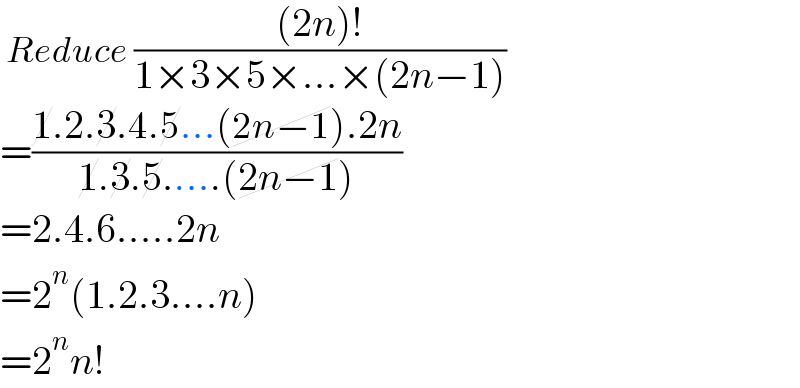
Reduce (((2n)!)/(1×3×5×...×(2n−1))) =((1.2.3.4.5...(2n−1).2n)/(1.3.5.....(2n−1))) =2.4.6.....2n =2^n (1.2.3....n) =2^n n!

$$\:{Reduce}\:\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{1}×\mathrm{3}×\mathrm{5}×...×\left(\mathrm{2}{n}−\mathrm{1}\right)}\: \\ $$$$=\frac{\cancel{\mathrm{1}}.\mathrm{2}.\cancel{\mathrm{3}}.\mathrm{4}.\cancel{\mathrm{5}}...\left(\cancel{\mathrm{2}{n}−\mathrm{1}}\right).\mathrm{2}{n}}{\cancel{\mathrm{1}}.\cancel{\mathrm{3}}.\cancel{\mathrm{5}}.....\left(\cancel{\mathrm{2}{n}−\mathrm{1}}\right)} \\ $$$$=\mathrm{2}.\mathrm{4}.\mathrm{6}.....\mathrm{2}{n} \\ $$$$=\mathrm{2}^{{n}} \left(\mathrm{1}.\mathrm{2}.\mathrm{3}....{n}\right) \\ $$$$=\mathrm{2}^{{n}} {n}! \\ $$

Commented by Acem last updated on 17/Oct/22

Good Sir!

$${Good}\:{Sir}!\: \\ $$

Commented by Acem last updated on 17/Oct/22

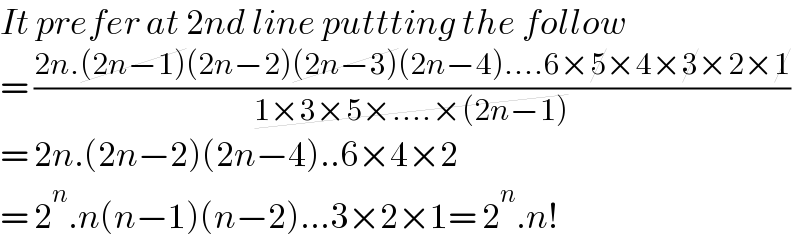
It prefer at 2nd line puttting the follow = ((2n.(2n−1)(2n−2)(2n−3)(2n−4)....6×5×4×3×2×1)/(1×3×5×....×(2n−1))) = 2n.(2n−2)(2n−4)..6×4×2 = 2^n .n(n−1)(n−2)...3×2×1= 2^n .n!

$${It}\:{prefer}\:{at}\:\mathrm{2}{nd}\:{line}\:{puttting}\:{the}\:{follow} \\ $$$$=\:\frac{\mathrm{2}{n}.\cancel{\left(\mathrm{2}{n}−\mathrm{1}\right)}\left(\mathrm{2}{n}−\mathrm{2}\right)\cancel{\left(\mathrm{2}{n}−\mathrm{3}\right)}\left(\mathrm{2}{n}−\mathrm{4}\right)....\mathrm{6}×\cancel{\mathrm{5}}×\mathrm{4}×\cancel{\mathrm{3}}×\mathrm{2}×\cancel{\mathrm{1}}}{\cancel{\mathrm{1}×\mathrm{3}×\mathrm{5}×....×\left(\mathrm{2}{n}−\mathrm{1}\right)}} \\ $$$$=\:\mathrm{2}{n}.\left(\mathrm{2}{n}−\mathrm{2}\right)\left(\mathrm{2}{n}−\mathrm{4}\right)..\mathrm{6}×\mathrm{4}×\mathrm{2} \\ $$$$=\:\mathrm{2}^{{n}} .{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\mathrm{3}×\mathrm{2}×\mathrm{1}=\:\mathrm{2}^{{n}} .{n}! \\ $$

Commented by Rasheed.Sindhi last updated on 17/Oct/22

Ok sir, thank you!

$$\mathrm{Ok}\:\mathrm{sir},\:\mathrm{thank}\:\mathrm{you}! \\ $$

Commented by Acem last updated on 17/Oct/22

The best Rasheed, thank you

$${The}\:{best}\:{Rasheed},\:{thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com