
Question Number 178375 by doline last updated on 16/Oct/22
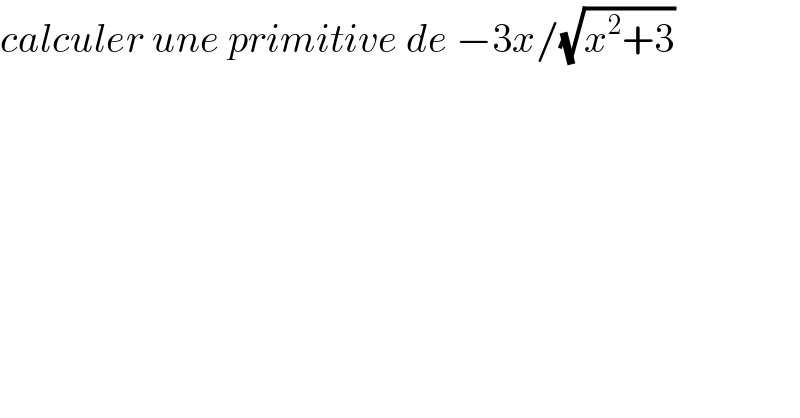
$${calculer}\:{une}\:{primitive}\:{de}\:−\mathrm{3}{x}/\sqrt{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$
Commented by CElcedricjunior last updated on 16/Oct/22
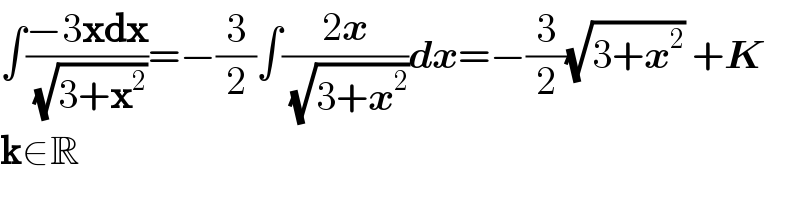
$$\int\frac{−\mathrm{3}\boldsymbol{\mathrm{xdx}}}{\:\sqrt{\mathrm{3}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}=−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{2}\boldsymbol{{x}}}{\:\sqrt{\mathrm{3}+\boldsymbol{{x}}^{\mathrm{2}} }}\boldsymbol{{dx}}=−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{3}+\boldsymbol{{x}}^{\mathrm{2}} }\:+\boldsymbol{{K}} \\ $$$$\boldsymbol{\mathrm{k}}\in\mathbb{R} \\ $$
Answered by Ar Brandon last updated on 16/Oct/22
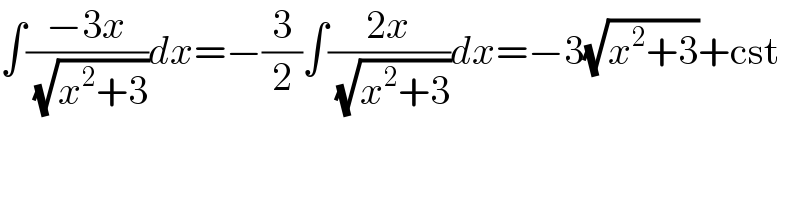
$$\int\frac{−\mathrm{3}{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{dx}=−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{dx}=−\mathrm{3}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}+\mathrm{cst} \\ $$
