
Question Number 178374 by depressiveshrek last updated on 16/Oct/22

$${Let}\:{the}\:{points}\:{ABC}\:{form}\:{a}\:{triangle}\:{on}\:{the} \\ $$$${cartesian}\:{plane},\:{whose}\:{area}\:{is}\:\mathrm{20}.\:{Let}\:{the}\:{coordinates} \\ $$$${of}\:{said}\:{points}\:{be}\:{A}\left(\mathrm{8},\:\mathrm{6}\right)\:{B}\left(\mathrm{2},\:\mathrm{4}\right)\:{and}\:{C}\left({x},\:{y}\right) \\ $$$${If}\:\mid{AC}\mid=\mid{BC}\mid,\:{find}\:{the}\:{coordinates}\:{of}\:{point}\:{C}. \\ $$
Answered by Ar Brandon last updated on 16/Oct/22

$$\mathrm{Let}\:{M}\:\mathrm{be}\:\mathrm{the}\:\mathrm{midpoint}\:\mathrm{of}\:{BC}.\:\mathrm{Then} \\ $$$${M}\:\mathrm{has}\:\mathrm{coordinates}\:\left(\frac{\mathrm{8}+\mathrm{2}}{\mathrm{2}},\:\frac{\mathrm{6}+\mathrm{4}}{\mathrm{2}}\right)={M}\left(\mathrm{5},\:\mathrm{5}\right) \\ $$$$\mathrm{If}\:\mid{AC}\mid=\mid{BC}\mid\:\mathrm{then}\:\Delta_{{ABC}} \:\mathrm{is}\:\mathrm{an}\:\mathrm{isosceles}\:\mathrm{triangle} \\ $$$$\mid{AM}\mid=\sqrt{\left(\mathrm{8}−\mathrm{5}\right)^{\mathrm{2}} +\left(\mathrm{6}−\mathrm{5}\right)^{\mathrm{2}} }=\sqrt{\mathrm{10}} \\ $$$$\mid{CM}\mid=\sqrt{\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} } \\ $$$$\mid{AC}\mid=\mid{BC}\mid \\ $$$$\Rightarrow\sqrt{\left({x}−\mathrm{8}\right)^{\mathrm{2}} +\left({y}−\mathrm{6}\right)^{\mathrm{2}} }=\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow−\mathrm{6}\left(\mathrm{2}{x}−\mathrm{10}\right)=\mathrm{2}\left(\mathrm{2}{y}−\mathrm{10}\right)\:\Rightarrow{y}−\mathrm{5}=−\mathrm{3}\left({x}−\mathrm{5}\right) \\ $$$$\Rightarrow\mid{CM}\mid=\sqrt{\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\mathrm{9}\left({x}−\mathrm{5}\right)^{\mathrm{2}} }=\sqrt{\mathrm{10}}\mid{x}−\mathrm{5}\mid \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{triangle}=\mathrm{20} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mid{AM}\mid\centerdot\mid{CM}\mid=\mathrm{20}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{10}}×\sqrt{\mathrm{10}}\mid{x}−\mathrm{5}\mid=\mathrm{10} \\ $$$$\Rightarrow{x}=\mathrm{7}\:\Rightarrow{y}−\mathrm{5}=−\mathrm{3}\left(\mathrm{7}−\mathrm{5}\right)\:\Rightarrow{y}=−\mathrm{1} \\ $$$$\mathrm{Hence}\:\mathrm{coordinates}\:\mathrm{of}\:{C}\:\mathrm{are}\:{C}\left(\mathrm{7},\:−\mathrm{1}\right) \\ $$
Commented by depressiveshrek last updated on 16/Oct/22
$${Correct},\:{but}\:{there}\:{is}\:{also}\:{another}\:{point}\:{of}\:{C}\:{that} \\ $$$${helps}\:{to}\:{form}\:{the}\:{triangle}. \\ $$
Commented by Ar Brandon last updated on 16/Oct/22
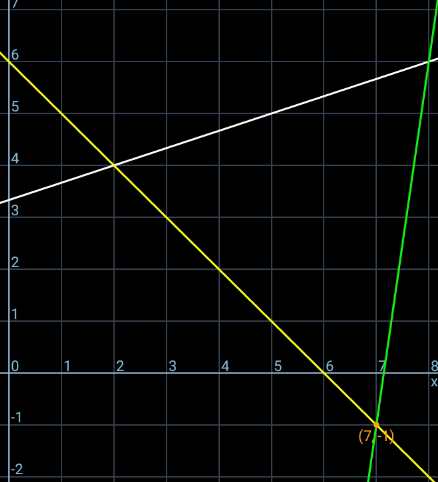
Commented by Ar Brandon last updated on 16/Oct/22
$$\mathrm{The}\:\mathrm{second}\:\mathrm{point}\:\mathrm{is}\:\mathrm{the}\:\mathrm{reflection}\:\mathrm{of}\:{C}_{\mathrm{1}} \:\mathrm{on}\:\mathrm{y}_{{AB}} \\ $$
Commented by Ar Brandon last updated on 16/Oct/22
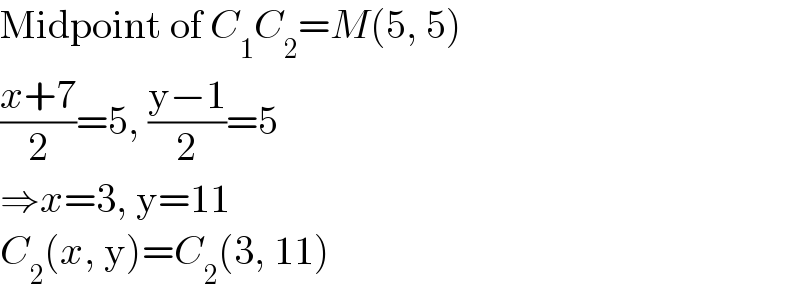
$$\mathrm{Midpoint}\:\mathrm{of}\:{C}_{\mathrm{1}} {C}_{\mathrm{2}} ={M}\left(\mathrm{5},\:\mathrm{5}\right) \\ $$$$\frac{{x}+\mathrm{7}}{\mathrm{2}}=\mathrm{5},\:\frac{\mathrm{y}−\mathrm{1}}{\mathrm{2}}=\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{3},\:\mathrm{y}=\mathrm{11} \\ $$$${C}_{\mathrm{2}} \left({x},\:\mathrm{y}\right)={C}_{\mathrm{2}} \left(\mathrm{3},\:\mathrm{11}\right) \\ $$
