
Question Number 178339 by a.lgnaoui last updated on 15/Oct/22

$${Determiner}\:{le}\:{temps}\:{necessaire}\:{pour} \\ $$$${remplir}\:{le}\:{verre}\:{a}\:{la}\:{hauteur}\:{h}. \\ $$
Commented by a.lgnaoui last updated on 15/Oct/22

Commented by CElcedricjunior last updated on 15/Oct/22
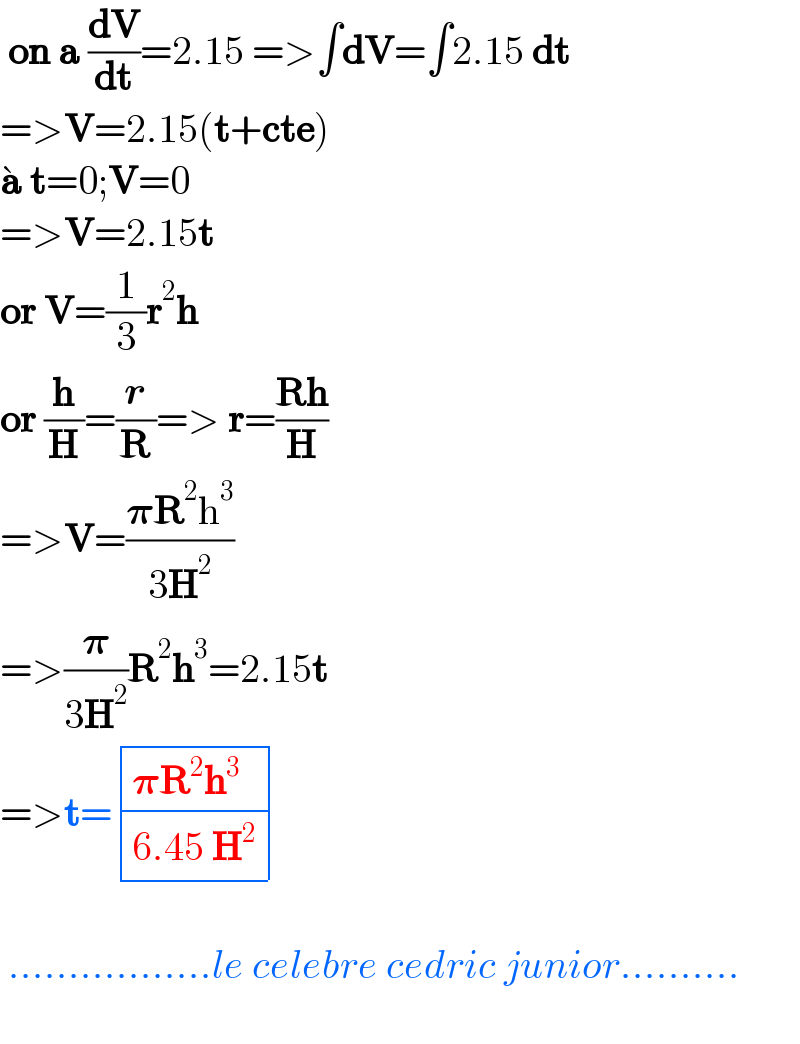
$$\:\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{a}}\:\frac{\boldsymbol{\mathrm{dV}}}{\boldsymbol{\mathrm{dt}}}=\mathrm{2}.\mathrm{15}\:=>\int\boldsymbol{\mathrm{dV}}=\int\mathrm{2}.\mathrm{15}\:\boldsymbol{\mathrm{dt}} \\ $$$$=>\boldsymbol{\mathrm{V}}=\mathrm{2}.\mathrm{15}\left(\boldsymbol{\mathrm{t}}+\boldsymbol{\mathrm{cte}}\right) \\ $$$$\grave {\boldsymbol{\mathrm{a}}}\:\boldsymbol{\mathrm{t}}=\mathrm{0};\boldsymbol{\mathrm{V}}=\mathrm{0} \\ $$$$=>\boldsymbol{\mathrm{V}}=\mathrm{2}.\mathrm{15}\boldsymbol{\mathrm{t}} \\ $$$$\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{V}}=\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{\mathrm{r}}^{\mathrm{2}} \boldsymbol{\mathrm{h}} \\ $$$$\boldsymbol{\mathrm{or}}\:\frac{\boldsymbol{\mathrm{h}}}{\boldsymbol{\mathrm{H}}}=\frac{\boldsymbol{{r}}}{\boldsymbol{\mathrm{R}}}=>\:\boldsymbol{\mathrm{r}}=\frac{\boldsymbol{\mathrm{Rh}}}{\boldsymbol{\mathrm{H}}}\: \\ $$$$=>\boldsymbol{\mathrm{V}}=\frac{\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} \mathrm{h}^{\mathrm{3}} }{\mathrm{3}\boldsymbol{\mathrm{H}}^{\mathrm{2}} } \\ $$$$=>\frac{\boldsymbol{\pi}}{\mathrm{3}\boldsymbol{\mathrm{H}}^{\mathrm{2}} }\boldsymbol{\mathrm{R}}^{\mathrm{2}} \boldsymbol{\mathrm{h}}^{\mathrm{3}} =\mathrm{2}.\mathrm{15}\boldsymbol{\mathrm{t}} \\ $$$$=>\boldsymbol{\mathrm{t}}=\begin{array}{|c|c|}{\boldsymbol{\pi\mathrm{R}}^{\mathrm{2}} \boldsymbol{\mathrm{h}}^{\mathrm{3}} }\\{\mathrm{6}.\mathrm{45}\:\boldsymbol{\mathrm{H}}^{\mathrm{2}} }\\\hline\end{array} \\ $$$$\: \\ $$$$\:.................{le}\:{celebre}\:{cedric}\:{junior}.......... \\ $$$$ \\ $$
Commented by Tawa11 last updated on 15/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by a.lgnaoui last updated on 16/Oct/22

$${thank}\:\:{you} \\ $$
Answered by Acem last updated on 15/Oct/22
![T= 77,93.10^(−3) .h^3 [min] ; T= ((πR^2 h^3 )/(3H^2 Q))](Q178343.png)
$$\:{T}=\:\mathrm{77},\mathrm{93}.\mathrm{10}^{−\mathrm{3}} .{h}^{\mathrm{3}} \:\left[{min}\right]\:\:;\:{T}=\:\frac{\pi{R}^{\mathrm{2}} {h}^{\mathrm{3}} }{\mathrm{3}{H}^{\mathrm{2}} {Q}} \\ $$
