
Question Number 178250 by zaheen last updated on 14/Oct/22
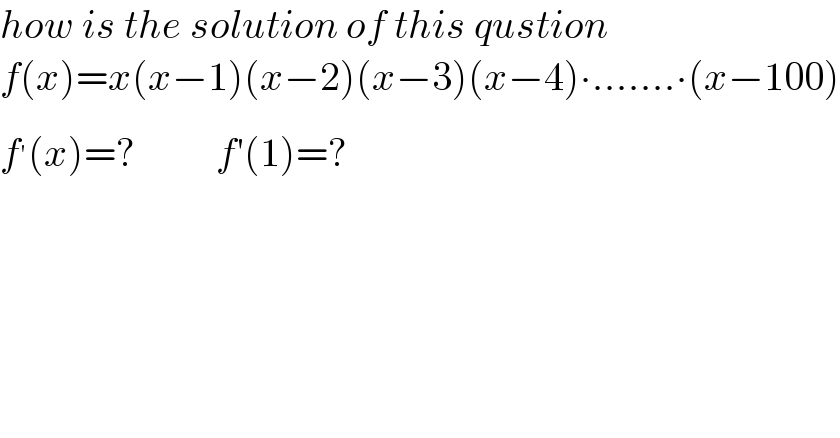
$${how}\:{is}\:{the}\:{solution}\:{of}\:{this}\:{qustion} \\ $$$${f}\left({x}\right)={x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\centerdot.......\centerdot\left({x}−\mathrm{100}\right) \\ $$$${f}^{'} \left({x}\right)=?\:\:\:\:\:\:\:\:\:\:{f}'\left(\mathrm{1}\right)=? \\ $$$$\:\: \\ $$
Answered by CElcedricjunior last updated on 14/Oct/22

$${f}\left({x}\right)=\boldsymbol{{x}}\left(\boldsymbol{{x}}−\mathrm{1}\right)\left(\boldsymbol{{x}}−\mathrm{2}\right)\left(\boldsymbol{{x}}−\mathrm{3}\right)....\left(\boldsymbol{{x}}−\boldsymbol{{n}}\right) \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}\boldsymbol{{x}}\left(\boldsymbol{{x}}−\boldsymbol{{k}}\right)=\boldsymbol{{x}}\left(\boldsymbol{{x}}−\mathrm{100}\right)! \\ $$$$\boldsymbol{{f}}'\left(\boldsymbol{{x}}\right)=\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}−\mathrm{2}\right)....\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{n}}\right)}{\boldsymbol{\mathrm{x}}}+ \\ $$$$\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}−\mathrm{2}\right)...\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{n}}\right)}{\boldsymbol{\mathrm{x}}−\mathrm{1}}+\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)...\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{n}}\right)}{\boldsymbol{\mathrm{x}}−\mathrm{2}} \\ $$$$+.....+\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}−\mathrm{2}\right)...\left(\boldsymbol{\mathrm{x}}−\mathrm{100}\right)}{\boldsymbol{\mathrm{x}}−\mathrm{100}} \\ $$$$\boldsymbol{{f}}'\left(\boldsymbol{{x}}\right)=\underset{\boldsymbol{{k}}=\mathrm{0}} {\overset{\mathrm{100}} {\sum}}\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}−\mathrm{100}\right)!}{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{k}}} \\ $$$$\boldsymbol{\mathrm{f}}'\left(\mathrm{1}\right)=\mathrm{1}×\left(−\mathrm{1}\right)×\left(−\mathrm{2}\right)×.....\left(\mathrm{1}−\mathrm{100}\right) \\ $$$$\boldsymbol{{f}}'\left(\mathrm{1}\right)=−\mathrm{99}! \\ $$$$........\:....{le}\:{celebre}\:\:{cedric}\:{junior}....... \\ $$
Answered by Sheshdevsahu last updated on 14/Oct/22
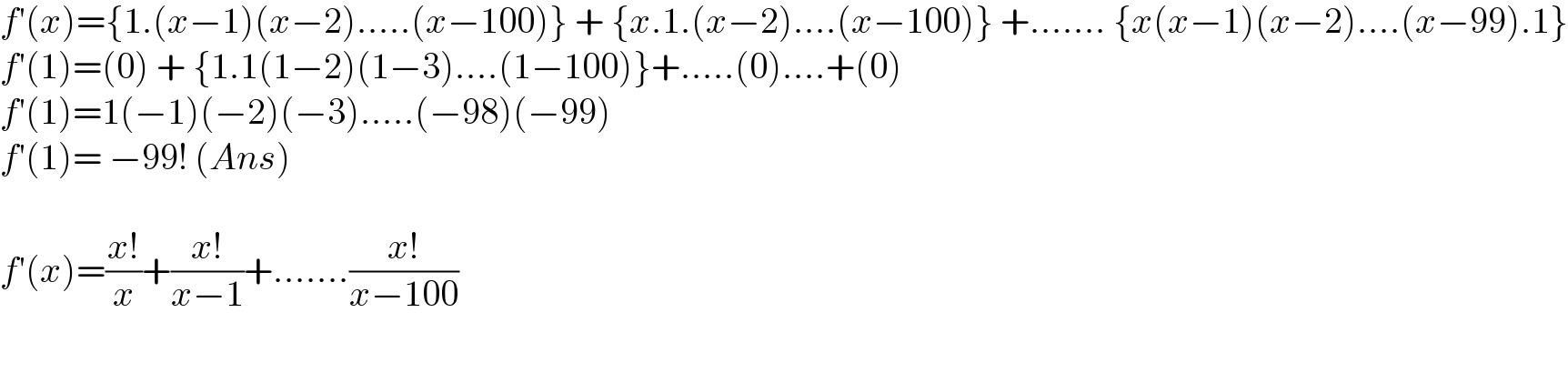
$${f}'\left({x}\right)=\left\{\mathrm{1}.\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right).....\left({x}−\mathrm{100}\right)\right\}\:+\:\left\{{x}.\mathrm{1}.\left({x}−\mathrm{2}\right)....\left({x}−\mathrm{100}\right)\right\}\:+.......\:\left\{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)....\left({x}−\mathrm{99}\right).\mathrm{1}\right\} \\ $$$${f}'\left(\mathrm{1}\right)=\left(\mathrm{0}\right)\:+\:\left\{\mathrm{1}.\mathrm{1}\left(\mathrm{1}−\mathrm{2}\right)\left(\mathrm{1}−\mathrm{3}\right)....\left(\mathrm{1}−\mathrm{100}\right)\right\}+.....\left(\mathrm{0}\right)....+\left(\mathrm{0}\right) \\ $$$${f}'\left(\mathrm{1}\right)=\mathrm{1}\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right).....\left(−\mathrm{98}\right)\left(−\mathrm{99}\right) \\ $$$${f}'\left(\mathrm{1}\right)=\:−\mathrm{99}!\:\left({Ans}\right) \\ $$$$ \\ $$$${f}'\left({x}\right)=\frac{{x}!}{{x}}+\frac{{x}!}{{x}−\mathrm{1}}+.......\frac{{x}!}{{x}−\mathrm{100}} \\ $$$$\:\:\:\:\:\:\:\: \\ $$
