
Question Number 184260 by Ml last updated on 04/Jan/23

$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=−\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{1377}} =? \\ $$
Answered by SEKRET last updated on 04/Jan/23
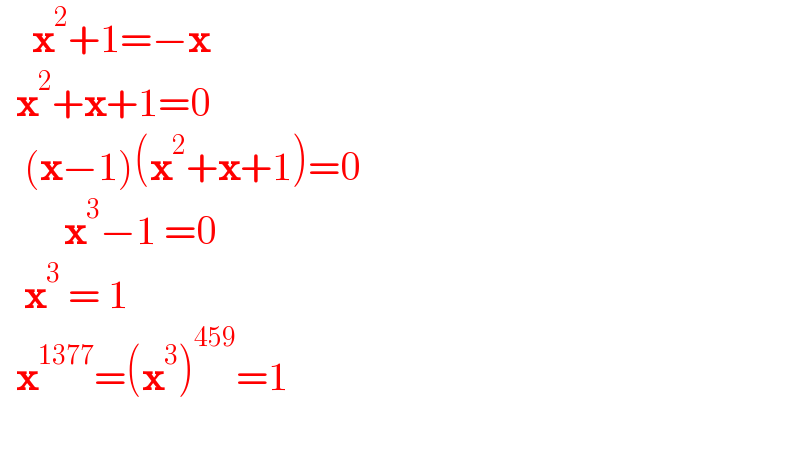
$$\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}=−\boldsymbol{\mathrm{x}} \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} −\mathrm{1}\:=\mathrm{0} \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:=\:\mathrm{1} \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\mathrm{1377}} =\left(\boldsymbol{\mathrm{x}}^{\mathrm{3}} \right)^{\mathrm{459}} =\mathrm{1} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 04/Jan/23
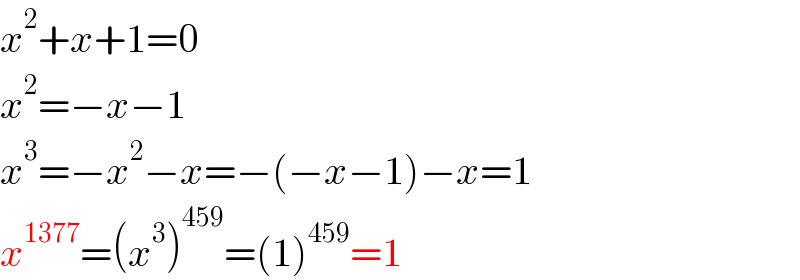
$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =−{x}−\mathrm{1} \\ $$$${x}^{\mathrm{3}} =−{x}^{\mathrm{2}} −{x}=−\left(−{x}−\mathrm{1}\right)−{x}=\mathrm{1} \\ $$$${x}^{\mathrm{1377}} =\left({x}^{\mathrm{3}} \right)^{\mathrm{459}} =\left(\mathrm{1}\right)^{\mathrm{459}} =\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 04/Jan/23
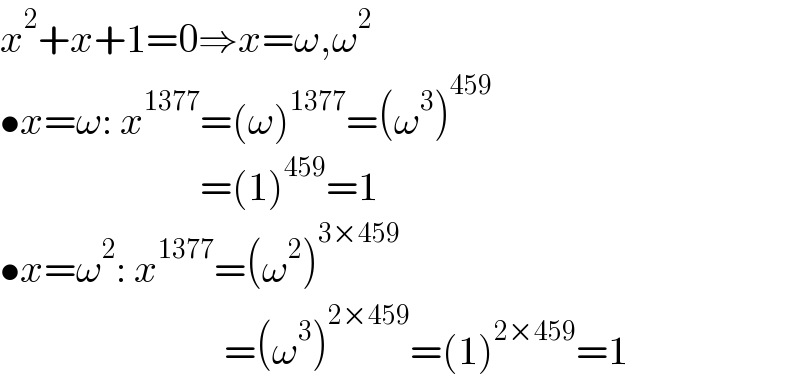
$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\omega,\omega^{\mathrm{2}} \\ $$$$\bullet{x}=\omega:\:{x}^{\mathrm{1377}} =\left(\omega\right)^{\mathrm{1377}} =\left(\omega^{\mathrm{3}} \right)^{\mathrm{459}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{1}\right)^{\mathrm{459}} =\mathrm{1} \\ $$$$\bullet{x}=\omega^{\mathrm{2}} :\:{x}^{\mathrm{1377}} =\left(\omega^{\mathrm{2}} \right)^{\mathrm{3}×\mathrm{459}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\omega^{\mathrm{3}} \right)^{\mathrm{2}×\mathrm{459}} =\left(\mathrm{1}\right)^{\mathrm{2}×\mathrm{459}} =\mathrm{1} \\ $$
