
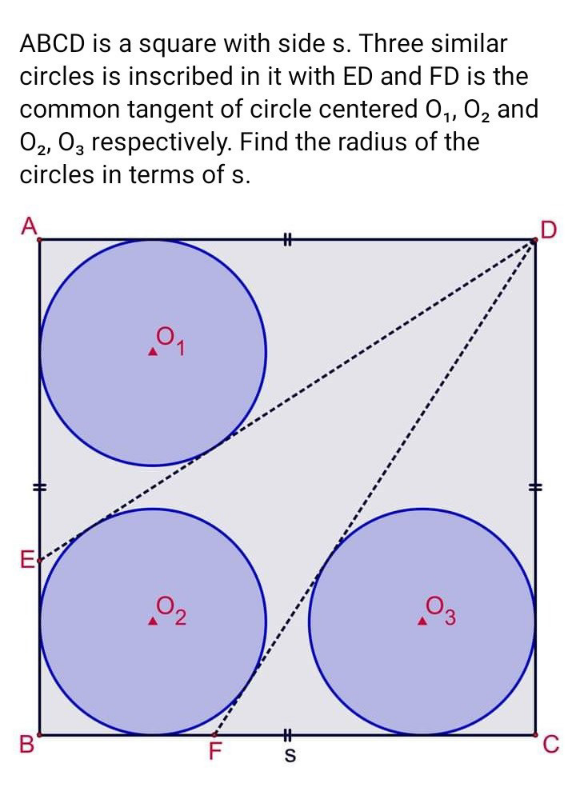
Question Number 178131 by cortano1 last updated on 13/Oct/22
Commented by Frix last updated on 13/Oct/22
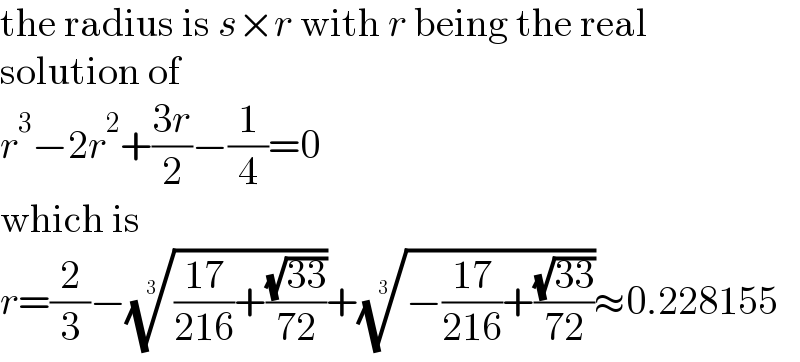
$$\mathrm{the}\:\mathrm{radius}\:\mathrm{is}\:{s}×{r}\:\mathrm{with}\:{r}\:\mathrm{being}\:\mathrm{the}\:\mathrm{real} \\ $$$$\mathrm{solution}\:\mathrm{of} \\ $$$${r}^{\mathrm{3}} −\mathrm{2}{r}^{\mathrm{2}} +\frac{\mathrm{3}{r}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{is} \\ $$$${r}=\frac{\mathrm{2}}{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{17}}{\mathrm{216}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{72}}}+\sqrt[{\mathrm{3}}]{−\frac{\mathrm{17}}{\mathrm{216}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{72}}}\approx\mathrm{0}.\mathrm{228155} \\ $$
Commented by Tawa11 last updated on 13/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 13/Oct/22
Commented by mr W last updated on 13/Oct/22
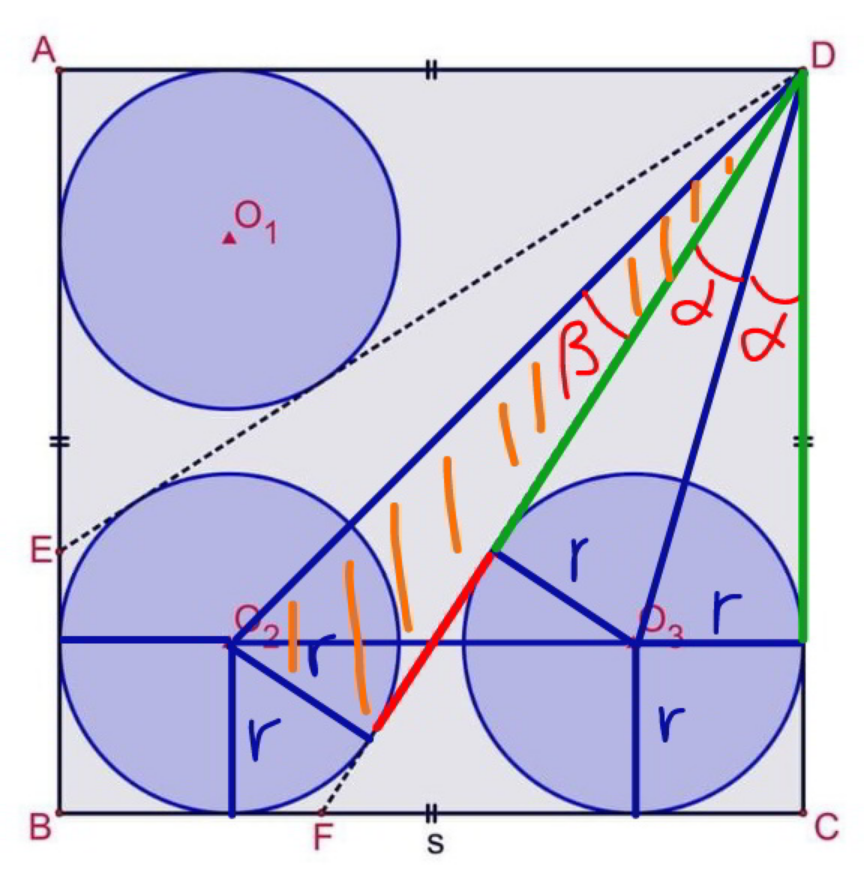
![let λ=(r/s) [(√2)(s−r)]^2 −r^2 =[s−r+(√((s−2r)^2 −(2r)^2 ))]^2 2(1−λ)^2 −λ^2 =[1−λ+(√((1−2λ)^2 −(2λ)^2 ))]^2 λ=(1−λ)(√(1−4λ)) λ^3 −2λ^2 +(3/2)λ−(1/4)=0 ⇒λ≈0.2282](Q178199.png)
$${let}\:\lambda=\frac{{r}}{{s}} \\ $$$$\left[\sqrt{\mathrm{2}}\left({s}−{r}\right)\right]^{\mathrm{2}} −{r}^{\mathrm{2}} =\left[{s}−{r}+\sqrt{\left({s}−\mathrm{2}{r}\right)^{\mathrm{2}} −\left(\mathrm{2}{r}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} −\lambda^{\mathrm{2}} =\left[\mathrm{1}−\lambda+\sqrt{\left(\mathrm{1}−\mathrm{2}\lambda\right)^{\mathrm{2}} −\left(\mathrm{2}\lambda\right)^{\mathrm{2}} }\right]^{\mathrm{2}} \\ $$$$\lambda=\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{1}−\mathrm{4}\lambda} \\ $$$$\lambda^{\mathrm{3}} −\mathrm{2}\lambda^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\lambda−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow\lambda\approx\mathrm{0}.\mathrm{2282} \\ $$
Commented by Tawa11 last updated on 14/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
