
Question Number 178115 by aurpeyz last updated on 12/Oct/22
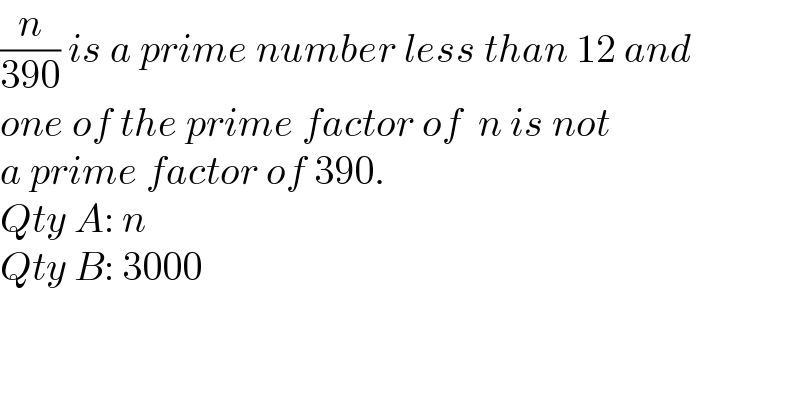
$$\frac{{n}}{\mathrm{390}}\:{is}\:{a}\:{prime}\:{number}\:{less}\:{than}\:\mathrm{12}\:{and}\: \\ $$$${one}\:{of}\:{the}\:{prime}\:{factor}\:{of}\:\:{n}\:{is}\:{not}\: \\ $$$${a}\:{prime}\:{factor}\:{of}\:\mathrm{390}. \\ $$$${Qty}\:{A}:\:{n} \\ $$$${Qty}\:{B}:\:\mathrm{3000} \\ $$
Answered by Rasheed.Sindhi last updated on 13/Oct/22

$$\frac{{n}}{\mathrm{390}}={m}\left(\in\mathbb{P}\right)<\mathrm{12} \\ $$$${n}=\mathrm{390}{m} \\ $$$${let}\:{p}\:{is}\:{a}\:{prime}\:{factor}\:{of}\:{n}\:{which}\:{is} \\ $$$${not}\:{a}\:{prime}\:{factor}\:{of}\:\mathrm{390}. \\ $$$${let}\:{n}={pq}\:\wedge\:{p}\:\mid\:{m} \\ $$$$\:\because\:{m}\in\mathbb{P}\:\:\:\:\:\:\:\:\:\:\therefore{p}={m} \\ $$$$\frac{{n}}{\mathrm{390}}={p}\:\wedge\:{p}\mid{n}\:{but}\:{p}\:\nmid\:\mathrm{390} \\ $$$$\therefore{p}\neq\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{6},\mathrm{10},\mathrm{13},\mathrm{15},\mathrm{26},\mathrm{30},\mathrm{39},\mathrm{65}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{78},\mathrm{130},\mathrm{195},\mathrm{390}\: \\ $$$${p}\left(<\mathrm{12}\right)=\mathrm{7},\mathrm{11} \\ $$$${n}=\mathrm{390}{p}=\mathrm{390}\centerdot\mathrm{7},\mathrm{390}\centerdot\mathrm{11} \\ $$$${n}=\mathrm{2730},\mathrm{4290} \\ $$
Commented by Tawa11 last updated on 13/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 13/Oct/22
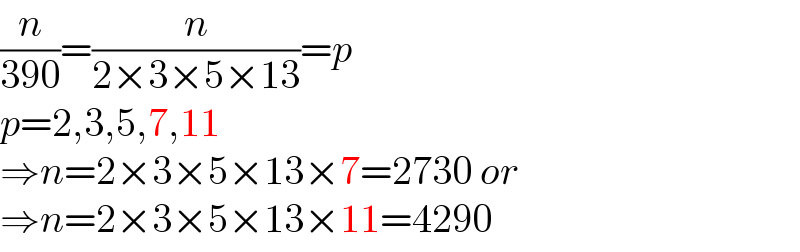
$$\frac{{n}}{\mathrm{390}}=\frac{{n}}{\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{13}}={p} \\ $$$${p}=\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7},\mathrm{11} \\ $$$$\Rightarrow{n}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{13}×\mathrm{7}=\mathrm{2730}\:{or} \\ $$$$\Rightarrow{n}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{13}×\mathrm{11}=\mathrm{4290} \\ $$
Commented by Rasheed.Sindhi last updated on 13/Oct/22

$$\underset{\underset{\overset{\:} {\mathrm{APPROACH}!}} {\overset{\:} {\mathrm{SMART}}}} {\mathrm{A}}\:\:\:\: \\ $$
