
Question Number 178114 by aurpeyz last updated on 12/Oct/22
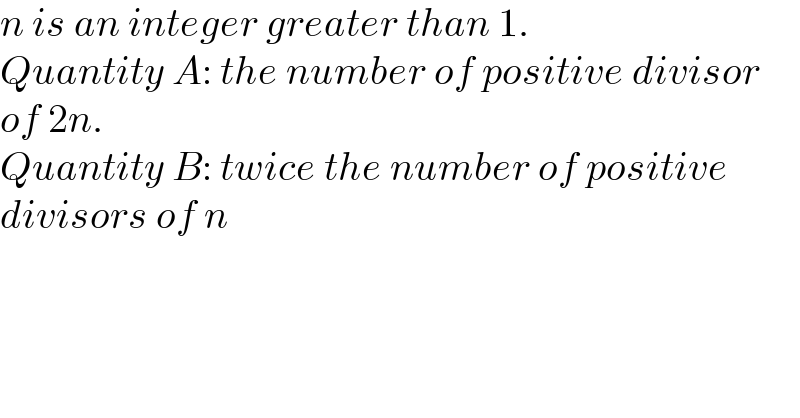
$${n}\:{is}\:{an}\:{integer}\:{greater}\:{than}\:\mathrm{1}. \\ $$$${Quantity}\:{A}:\:{the}\:{number}\:{of}\:{positive}\:{divisor} \\ $$$${of}\:\mathrm{2}{n}. \\ $$$${Quantity}\:{B}:\:{twice}\:{the}\:{number}\:{of}\:{positive} \\ $$$${divisors}\:{of}\:{n} \\ $$
Commented by mr W last updated on 13/Oct/22

$${what}\:{is}\:{asked}? \\ $$
Answered by mr W last updated on 13/Oct/22
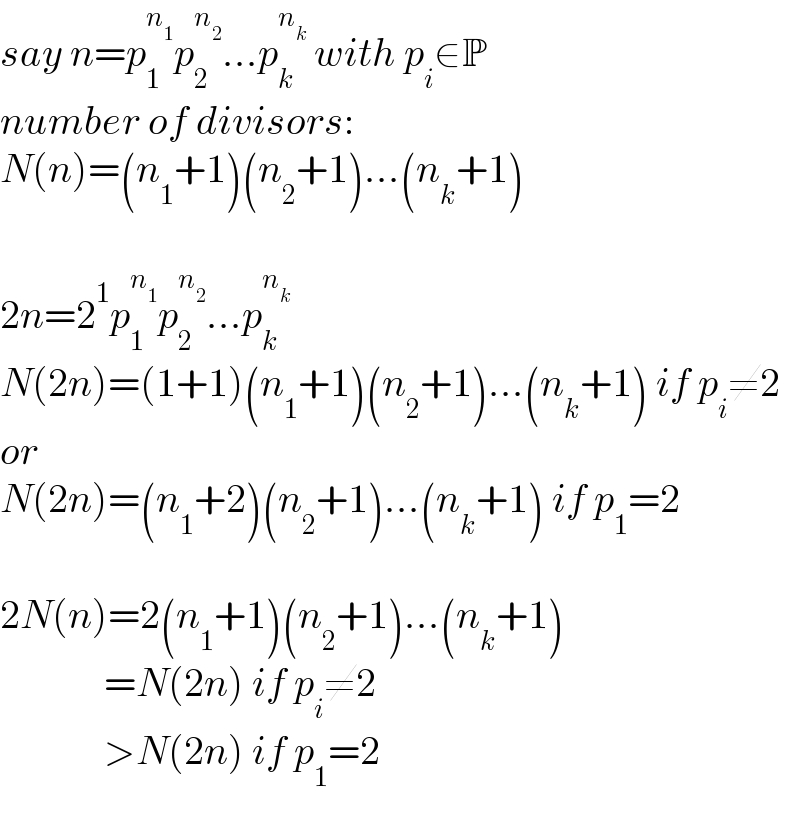
$${say}\:{n}={p}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{n}_{\mathrm{2}} } ...{p}_{{k}} ^{{n}_{{k}} } \:{with}\:{p}_{{i}} \in\mathbb{P} \\ $$$${number}\:{of}\:{divisors}: \\ $$$${N}\left({n}\right)=\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)...\left({n}_{{k}} +\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{2}{n}=\mathrm{2}^{\mathrm{1}} {p}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{n}_{\mathrm{2}} } ...{p}_{{k}} ^{{n}_{{k}} } \\ $$$${N}\left(\mathrm{2}{n}\right)=\left(\mathrm{1}+\mathrm{1}\right)\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)...\left({n}_{{k}} +\mathrm{1}\right)\:{if}\:{p}_{{i}} \neq\mathrm{2} \\ $$$${or} \\ $$$${N}\left(\mathrm{2}{n}\right)=\left({n}_{\mathrm{1}} +\mathrm{2}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)...\left({n}_{{k}} +\mathrm{1}\right)\:{if}\:{p}_{\mathrm{1}} =\mathrm{2} \\ $$$$ \\ $$$$\mathrm{2}{N}\left({n}\right)=\mathrm{2}\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)...\left({n}_{{k}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={N}\left(\mathrm{2}{n}\right)\:{if}\:{p}_{{i}} \neq\mathrm{2}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:>{N}\left(\mathrm{2}{n}\right)\:{if}\:{p}_{\mathrm{1}} =\mathrm{2}\:\:\:\:\: \\ $$
Commented by aurpeyz last updated on 13/Oct/22

$${a}.\:{Quantity}\:{A}\:{is}\:{greater}\:{than}\:{B} \\ $$$${b}.\:{Quantity}\:{B}\:{is}\:{greater}\:{than}\:{A} \\ $$$${c}\:.\:{they}\:{are}\:{equal} \\ $$$${d}.\:{Cannot}\:{be}\:{determined}\:{by}\:{the}\:{given} \\ $$$${information} \\ $$
Commented by mr W last updated on 13/Oct/22

$${answer}\:{d} \\ $$
Commented by mr W last updated on 13/Oct/22

$${example}\:\mathrm{1}:\:{n}=\mathrm{15} \\ $$$${n}=\mathrm{15}\:{has}\:\mathrm{4}\:{divisors}:\:\mathrm{1},\mathrm{3},\mathrm{5},\mathrm{15} \\ $$$$\mathrm{2}{n}=\mathrm{30}\:{has}\:\mathrm{8}\:{divisors}:\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{15},\mathrm{30} \\ $$$${Qnt}.\:{A}=\mathrm{8} \\ $$$${Qnt}.{B}=\mathrm{2}×\mathrm{4}=\mathrm{8} \\ $$$${Qnt}.\:{A}={Qnt}.\:{B} \\ $$$$ \\ $$$${example}\:\mathrm{2}:\:{n}=\mathrm{10} \\ $$$${n}=\mathrm{10}\:{has}\:\mathrm{4}\:{divisors}:\:\mathrm{1},\mathrm{2},\mathrm{5},\mathrm{10} \\ $$$$\mathrm{2}{n}=\mathrm{20}\:{has}\:\mathrm{6}\:{divisors}:\:\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{5},\mathrm{10},\mathrm{20} \\ $$$${Qnt}.\:{A}=\mathrm{6} \\ $$$${Qnt}.\:{B}=\mathrm{2}×\mathrm{4}=\mathrm{8} \\ $$$${Qnt}.\:{A}<{Qnt}.\:{B} \\ $$
Commented by Tawa11 last updated on 13/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by aurpeyz last updated on 18/Oct/22

$${thanks}\:{sir} \\ $$
