
Question Number 177933 by Spillover last updated on 11/Oct/22
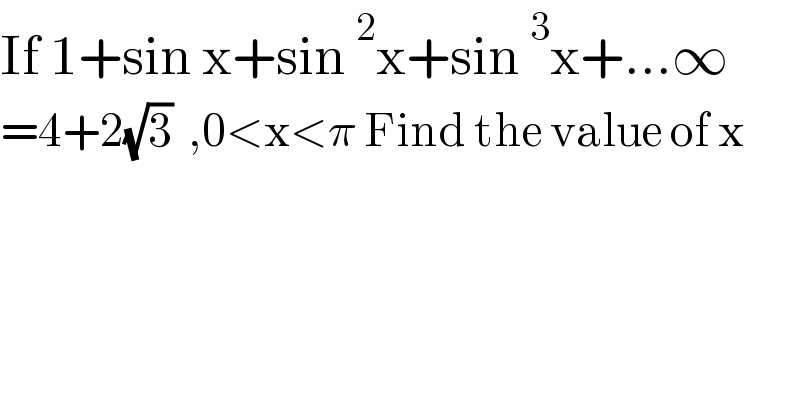
$$\mathrm{If}\:\mathrm{1}+\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+...\infty \\ $$ $$=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\:\:,\mathrm{0}<\mathrm{x}<\pi\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$ $$ \\ $$
Answered by Ar Brandon last updated on 11/Oct/22
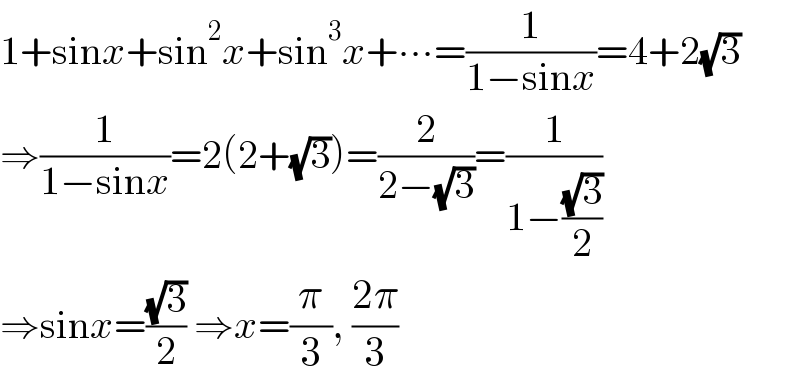
$$\mathrm{1}+\mathrm{sin}{x}+\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{3}} {x}+\centerdot\centerdot\centerdot=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}{x}}=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$ $$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}{x}}=\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)=\frac{\mathrm{2}}{\mathrm{2}−\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$ $$\Rightarrow\mathrm{sin}{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow{x}=\frac{\pi}{\mathrm{3}},\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$
Commented bySpillover last updated on 11/Oct/22

$${thanks}\:{for}\:{solving} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Oct/22
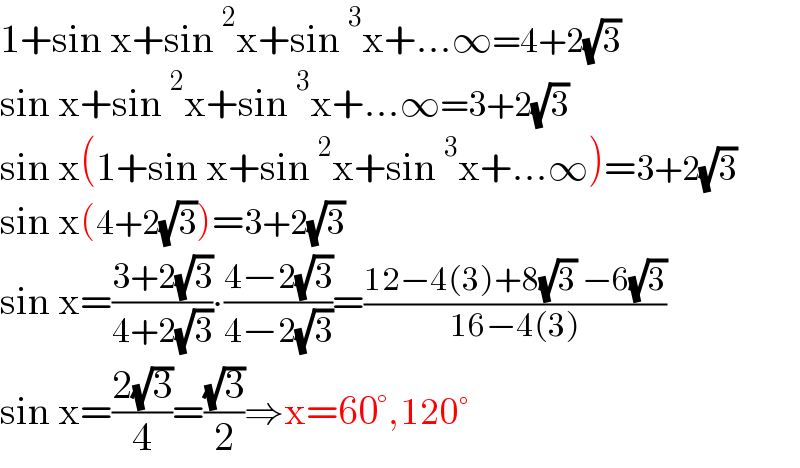
$$\mathrm{1}+\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+...\infty=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$ $$\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+...\infty=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$ $$\mathrm{sin}\:\mathrm{x}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+...\infty\right)=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$ $$\mathrm{sin}\:\mathrm{x}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$ $$\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}\centerdot\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\mathrm{12}−\mathrm{4}\left(\mathrm{3}\right)+\mathrm{8}\sqrt{\mathrm{3}}\:−\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{16}−\mathrm{4}\left(\mathrm{3}\right)} \\ $$ $$\mathrm{sin}\:\mathrm{x}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow\mathrm{x}=\mathrm{60}°,\mathrm{120}° \\ $$
Commented bySpillover last updated on 11/Oct/22
$$\mathrm{nice}\:\mathrm{solution} \\ $$
