
Question Number 177793 by cortano1 last updated on 09/Oct/22
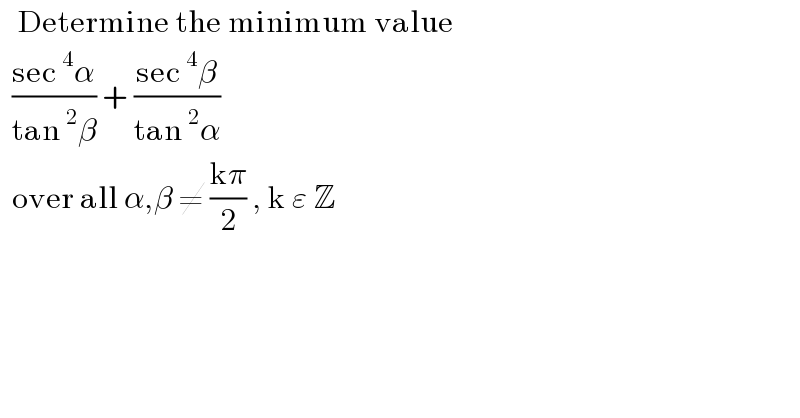
$$\:\:\:\mathrm{Determine}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value} \\ $$$$\:\:\frac{\mathrm{sec}\:^{\mathrm{4}} \alpha}{\mathrm{tan}\:^{\mathrm{2}} \beta}\:+\:\frac{\mathrm{sec}\:^{\mathrm{4}} \beta}{\mathrm{tan}\:^{\mathrm{2}} \alpha}\: \\ $$$$\:\:\mathrm{over}\:\mathrm{all}\:\alpha,\beta\:\neq\:\frac{\mathrm{k}\pi}{\mathrm{2}}\:,\:\mathrm{k}\:\varepsilon\:\mathbb{Z}\: \\ $$
Answered by mahdipoor last updated on 09/Oct/22
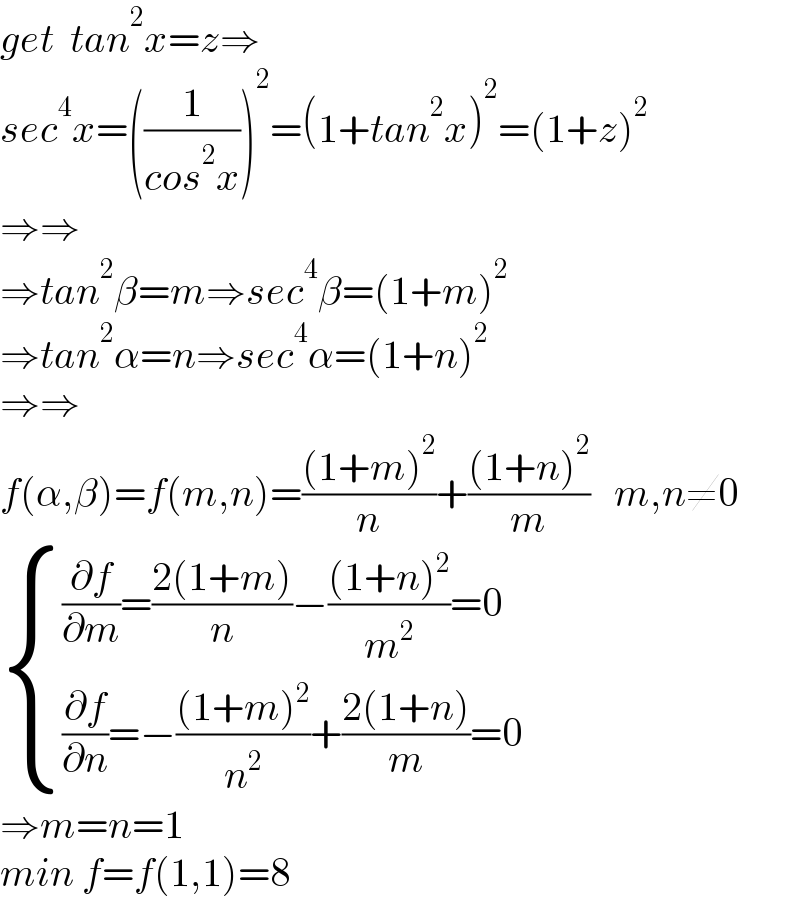
$${get}\:\:{tan}^{\mathrm{2}} {x}={z}\Rightarrow \\ $$$${sec}^{\mathrm{4}} {x}=\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\right)^{\mathrm{2}} =\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} =\left(\mathrm{1}+{z}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\Rightarrow \\ $$$$\Rightarrow{tan}^{\mathrm{2}} \beta={m}\Rightarrow{sec}^{\mathrm{4}} \beta=\left(\mathrm{1}+{m}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{tan}^{\mathrm{2}} \alpha={n}\Rightarrow{sec}^{\mathrm{4}} \alpha=\left(\mathrm{1}+{n}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\Rightarrow \\ $$$${f}\left(\alpha,\beta\right)={f}\left({m},{n}\right)=\frac{\left(\mathrm{1}+{m}\right)^{\mathrm{2}} }{{n}}+\frac{\left(\mathrm{1}+{n}\right)^{\mathrm{2}} }{{m}}\:\:\:{m},{n}\neq\mathrm{0} \\ $$$$\begin{cases}{\frac{\partial{f}}{\partial{m}}=\frac{\mathrm{2}\left(\mathrm{1}+{m}\right)}{{n}}−\frac{\left(\mathrm{1}+{n}\right)^{\mathrm{2}} }{{m}^{\mathrm{2}} }=\mathrm{0}}\\{\frac{\partial{f}}{\partial{n}}=−\frac{\left(\mathrm{1}+{m}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }+\frac{\mathrm{2}\left(\mathrm{1}+{n}\right)}{{m}}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow{m}={n}=\mathrm{1} \\ $$$${min}\:{f}={f}\left(\mathrm{1},\mathrm{1}\right)=\mathrm{8} \\ $$
