
Question Number 177741 by infinityaction last updated on 08/Oct/22

Answered by Frix last updated on 08/Oct/22
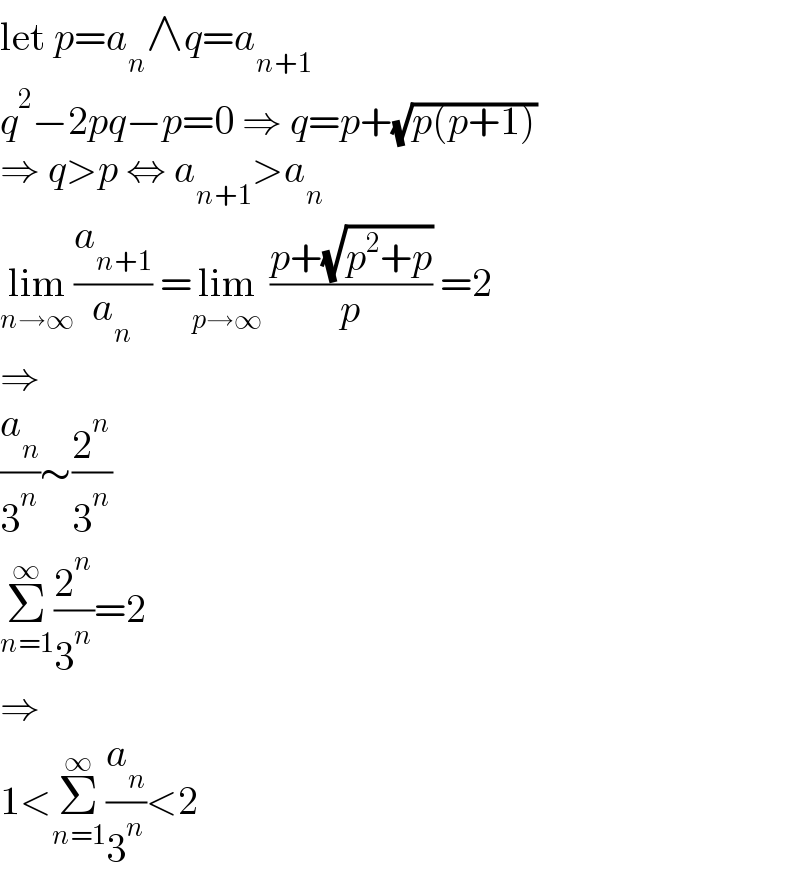
$$\mathrm{let}\:{p}={a}_{{n}} \wedge{q}={a}_{{n}+\mathrm{1}} \\ $$$${q}^{\mathrm{2}} −\mathrm{2}{pq}−{p}=\mathrm{0}\:\Rightarrow\:{q}={p}+\sqrt{{p}\left({p}+\mathrm{1}\right)} \\ $$$$\Rightarrow\:{q}>{p}\:\Leftrightarrow\:{a}_{{n}+\mathrm{1}} >{a}_{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }\:=\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\frac{{p}+\sqrt{{p}^{\mathrm{2}} +{p}}}{{p}}\:=\mathrm{2} \\ $$$$\Rightarrow \\ $$$$\frac{{a}_{{n}} }{\mathrm{3}^{{n}} }\sim\frac{\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} }=\mathrm{2} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}<\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{3}^{{n}} }<\mathrm{2} \\ $$
Commented by infinityaction last updated on 08/Oct/22

$${thanks}\:{sir} \\ $$
Answered by mr W last updated on 08/Oct/22
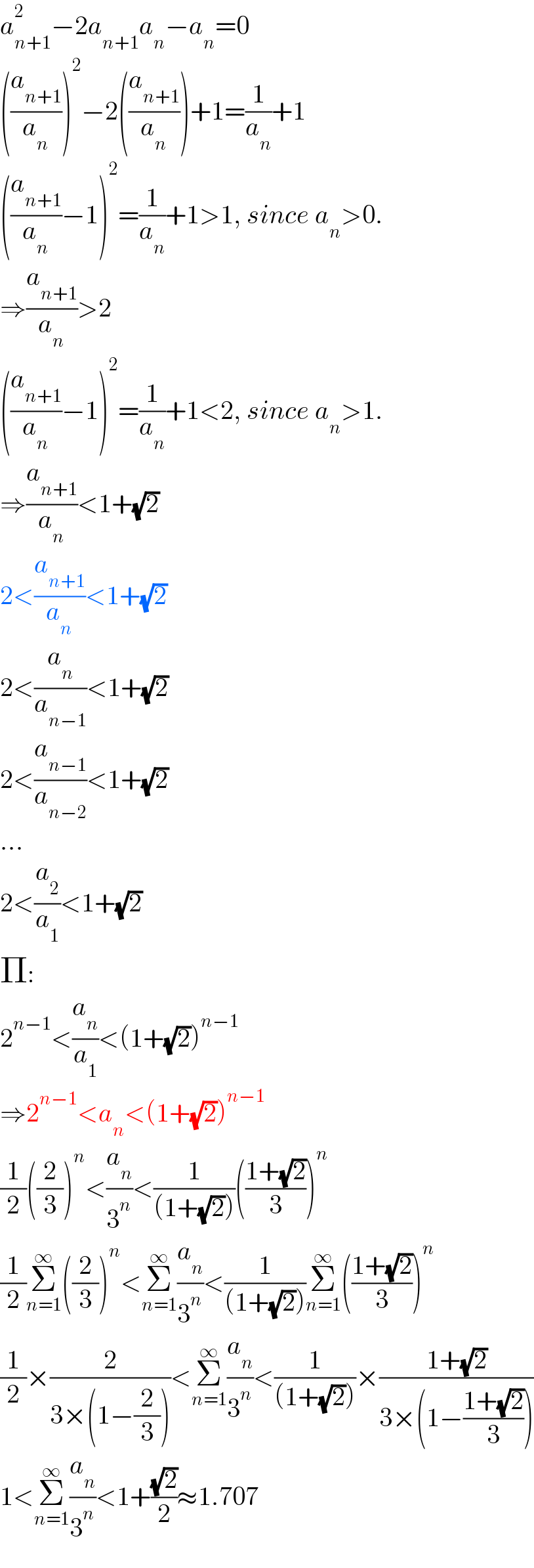
$${a}_{{n}+\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{a}_{{n}+\mathrm{1}} {a}_{{n}} −{a}_{{n}} =\mathrm{0} \\ $$$$\left(\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }\right)+\mathrm{1}=\frac{\mathrm{1}}{{a}_{{n}} }+\mathrm{1} \\ $$$$\left(\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }−\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{a}_{{n}} }+\mathrm{1}>\mathrm{1},\:{since}\:{a}_{{n}} >\mathrm{0}. \\ $$$$\Rightarrow\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }>\mathrm{2} \\ $$$$\left(\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }−\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{a}_{{n}} }+\mathrm{1}<\mathrm{2},\:{since}\:{a}_{{n}} >\mathrm{1}. \\ $$$$\Rightarrow\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }<\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{2}<\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }<\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{2}<\frac{{a}_{{n}} }{{a}_{{n}−\mathrm{1}} }<\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{2}<\frac{{a}_{{n}−\mathrm{1}} }{{a}_{{n}−\mathrm{2}} }<\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$... \\ $$$$\mathrm{2}<\frac{{a}_{\mathrm{2}} }{{a}_{\mathrm{1}} }<\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\Pi: \\ $$$$\mathrm{2}^{{n}−\mathrm{1}} <\frac{{a}_{{n}} }{{a}_{\mathrm{1}} }<\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}^{{n}−\mathrm{1}} <{a}_{{n}} <\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} <\frac{{a}_{{n}} }{\mathrm{3}^{{n}} }<\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} <\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{3}^{{n}} }<\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}×\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right)}<\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{3}^{{n}} }<\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}×\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{3}×\left(\mathrm{1}−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{3}}\right)} \\ $$$$\mathrm{1}<\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{\mathrm{3}^{{n}} }<\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\approx\mathrm{1}.\mathrm{707} \\ $$
Commented by infinityaction last updated on 08/Oct/22

$${thanks}\:{sir} \\ $$
Commented by Tawa11 last updated on 09/Oct/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
